练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

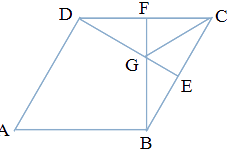
    【题目】如图，边长为2的菱形ABCD中，∠A=60°，E、F分别是BC，DC的中点，G为 BF、DE的交点，若 =

    （1）试用 ， 表示 ， ， ；
    （2）求 的值．

    【答案】
    （1）解：由题意， = + = + = + = +

    = + = + = ﹣ = ﹣ ，

    E、F分别是BC，DC的中点，G为 BF、DE的交点

    所以G为△BCD的重心，设BD中点为H，则

    = = × =﹣ =﹣ （ + ）=﹣ ﹣


    （2）解：

    =

    = ﹣ | || |cos60°﹣

    = ×4﹣ ×2×2× ﹣ ×4

    =﹣1．


    【解析】（1）由题意，根据平面向量的线性表示与运算法则，用 、 表示出 、 与 ；（2）根据平面向量的数量积运算，求出 即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】学校为了解学生在课外读物方面的支出情况，抽取了n名同学进行调查，结果显示这些同学的支出都在[10,50)(单位：元)，其中支出在[30,50)(单位：元)的同学有67人，其频率分布直方图如图所示，则n的值为(　　)

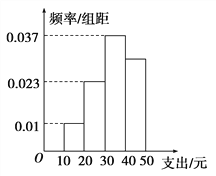
    A. 100 B. 120 C. 130 D. 390

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某书店销售刚刚上市的某知名品牌的高三数学单元卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如下数据：

    单价（元）

    18

    19

    20

    21

    22

    销量（册）

    61

    56

    50

    48

    45

    （1）求试销5天的销量的方差和对的回归直线方程；

    （2）预计今后的销售中，销量与单价服从（1）中的回归方程，已知每册单元卷的成本是14元，为了获得最大利润，该单元卷的单价卷的单价应定为多少元？

    （附：）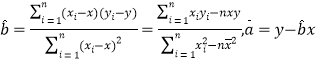

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】解答
    （1）在区间[1，3]上任取两整数a、b，求二次方程x2+2ax+b2=0有实数根的概率．
    （2）在区间[1，3]上任取两实数a、b，求二次方程x2+2ax+b2=0有实数根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近期中央电视台播出的《中国诗词大会》火遍全国，下面是组委会在选拔赛时随机抽取的100名选手的成绩，按成绩分组，得到的频率分布表如下所示：

    组号

    分组

    频数

    频率

    第1组

    第2组

    ①

    第3组

    20

    ②

    第4组

    20

    第5组

    10

    合计

    100

    （1）请先求出频率分布表中①、②位置的相应数据，再完成频率分布直方图（用阴影表示）；

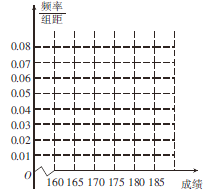
    （2）为了能选拔出最优秀的选手，组委会决定在笔试成绩高的第3、4、5组中用分层抽样抽取5名选手进入第二轮面试，求第3、4、5组每组各抽取多少名选手进入第二轮面试；

    （3）在（2）的前提下，组委会决定在5名选手中随机抽取2名选手接受考官进行面试，求：第4组至少有一名选手被考官面试的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在高中学习过程中，同学们经常这样说：“如果物理成绩好，那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究，得到了学生的物理成绩与数学成绩具有线性相关关系的结论.现从该班随机抽取5名学生在一次考试中的物理和数学成绩，如下表：

    编号

    成绩

    1

    2

    3

    4

    5

    物理（）

    90

    85

    74

    68

    63

    数学（）

    130

    125

    110

    95

    90

    （1）求数学成绩关于物理成绩的线性回归方程（精确到），若某位学生的物理成绩为80分，预测他的数学成绩；

    （2）要从抽取的五位学生中随机选出三位参加一项知识竞赛，以表示选中的学生的数学成绩高于100分的人数，求随机变量的分布列及数学期望.

    （参数公式： ， .）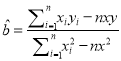

    参考数据： ，

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（x+φ）（A＞0，0＜φ＜π），x∈R的最大值是1，其图象经过点 ．
    （1）求f（x）的解析式；
    （2）已知 ，且 ， ，求f（α﹣β）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方形中， 的中点为点， 的中点为点，沿将向上折起得到，使得面面，此时点位于点处．

    （Ⅰ）证明： ；

    （Ⅱ）求面与面所成二面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC中，角A，B，C的对边分别是a，b，c，且2cos2 = sinB，a=3c．
    （1）求角B的大小和tanC的值；
    （2）若b=1，求△ABC的面积．

    查看答案和解析>>

    同步练习册答案