(1)已知命题p:2x2-3x+1≤0和命题q:x2-(2a+1)x+a(a+1)≤0,若¬p是¬q的必要不充分条件,求实数a的取值范围.
(2)已知命题s:方程x2+(m-3)x+m=0的一根在(0,1)内,另一根在(2,3)内.命题t:函数f(x)=ln(mx2-2x+1)的定义域为全体实数.若s∨t为真命题,求实数m的取值范围.
【答案】
分析:(1)求出命题p,q的等价形式,利用¬p是¬q的必要不充分条件,求出a的取值范围.
(2)求出命题s,t的等价形式,利用s∨t为真命题,求实数m的取值范围.
解答:解:(1)对于命题p:2x
2-3x+1≤0,解得:
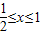
…(1分)
对于命题q:x
2-(2a+1)x+a(a+1)≤0,解得:a≤x≤a+1…(3分)
由¬p是¬q的必要不充分条件,所以¬q⇒¬p且¬p推不出¬q.于是所以p推不出q且q⇒p.…(5分)
所以
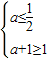
.解得

,即:
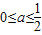
所以实数a的取值范围是
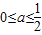
.…(7分)
(2)对于命题命题s:方程x
2+(m-3)x+m=0的一根在(0,1)内,另一根在(2,3)内,
设g(x)=x
2+(m-3)x+m,则:
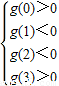
,即:
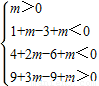
…(9分)
解得:
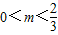
…(10分)
对于命题命题t:函数f(x)=ln(mx
2-2x+1)的定义域为全体实数,
则有:
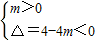
…(12分)
解得:m>1…(13分)
又s∨t为真命题,即s为真命题或t为真命题.
所以所求实数m的取值范围为
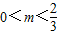
或m>1.…(14分)
点评:本题主要考查复合命题的真假应用,以及充分条件和必要条件的判断,考查学生的综合能力.

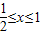 …(1分)
…(1分)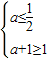 .解得
.解得 ,即:
,即: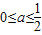
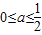 .…(7分)
.…(7分)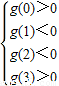 ,即:
,即: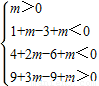 …(9分)
…(9分)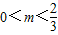 …(10分)
…(10分)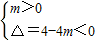 …(12分)
…(12分)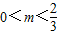 或m>1.…(14分)
或m>1.…(14分)

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案