
| 喜欢甜品 | 不喜欢甜品 | 合计 | |
| 南方学生 | a | 20 | 80 |
| 北方学生 | 10 | b | 20 |
| 合计 | 70 | 30 | 100 |
| P(K2≥k0) | 0.100 | 0.050 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
分析 (1)根据2×2列联表,求a、b;
(2)将2×2列联表中的数据代入公式计算,得K2的值,然后与表格中数据比较,则有在犯错误的概率不超过0.05的前提下可以认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
解答 解:(1)a=80-20=60、b=20-10=10;
(2)将2×2列联表中的数据代入计算公式,
得K2的观测值k=$\frac{100(60×10-20×10)2}{70×30×80×20}$=$\frac{100}{21}$≈4.762.
由于4.762>3.841,所以在犯错误的概率不超过0.05的前提下可以认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”.
点评 本题考查独立性检验的应用,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
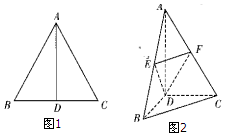 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${log_{0.7}}6<{0.7^6}<{6^{0.7}}$ | B. | 0.76<60.7<log0.76 | ||
| C. | ${log_{0.7}}6<{6^{0.7}}<{0.7^6}$ | D. | ${0.7^6}<{log_{0.7}}6<{6^{0.7}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “若m>0,则方程x2+x-m=0有两个不同的实数根”是真命题. | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0”. | |
| C. | 若命题p:?x∈R,x2+x+1>0,则?p:?x∈R,x2+x+1≤0. | |
| D. | 若p∧q为假命题,则p,q均为假命题. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+b2≠0 | B. | ab=0 | C. | a=0,b≠0 | D. | a≠0,b=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com