练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在中，角所对的边分别为，且．

    （1）求的值；

    （2）若，求的面积的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河南新乡一中高三文周考12.18数学试卷（解析版） 题型：解答题

    已知圆与轴交于0，两点，圆过0，两点，且直线与圆相切；

    （1）求圆的方程；

    （2）若圆上一动点，直线与圆的另一交点为，在平面内是否存在定点使得始终成立，若存在求出定点坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2017届云南大理州高三文上学期统测一数学试卷（解析版） 题型：解答题

    选修4-5：不等式选讲

    已知函数.

    （1）解关于的不等式；

    （2）设，试比较与的大小.

    查看答案和解析>>

    科目：高中数学 来源：2017届云南大理州高三文上学期统测一数学试卷（解析版） 题型：选择题

    已知向量与的夹角为30°，且，则等于（ ）

    A． B．3

    C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届云南大理州高三理上学期统测一数学试卷（解析版） 题型：解答题

    选修4-4：坐标系与参数方程

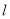    已知在直角坐标系中，曲线的参数方程为（为参数），现以原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为．

    （1）求曲线的普通方程和直线的直角坐标方程；

    （2）在曲线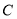上是否存在一点，使点到直线的距离最小？若存在，求出距离的最小值及点的直角坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源：2017届云南大理州高三理上学期统测一数学试卷（解析版） 题型：选择题

    定义在上的函数的导函数为，若对任意实数，有，且为奇函数，则不等式的解集是（ ）

    A． B．

    C． D．

    查看答案和解析>>

    科目：高中数学 来源：2017届云南大理州高三理上学期统测一数学试卷（解析版） 题型：选择题

    已知向量与的夹角为30°，且，则等于（ ）

    A．1 B．

    C．13 D．

    查看答案和解析>>

    科目：高中数学 来源：2017届四川凉山州高三文上学期一诊考试数学试卷（解析版） 题型：选择题

    公元263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后面两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出的值为（ ）

    （参考数据：，，）

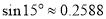    A．12 B．24 C．36 D．48

    查看答案和解析>>

    科目：高中数学 来源：2017届山东潍坊市高三文上学期期中联考数学试卷（解析版） 题型：填空题

    一艘海警船从港口出发，以每小时40海里的速度沿南偏东方向直线航行，30分钟后到达处，这时候接到从处发出的一求救信号，已知在的北偏东，港口的东偏南处，那么，两点的距离是 海里．

    查看答案和解析>>

    同步练习册答案