练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若实数x，y满足约束条件
    x+y≥0
    x-y+3≥0
    0≤x≤3
    ，则z=2x-y    的最大值为（　　）
    A、-
    9
    2
    B、11
    C、0
    D、9
    分析：首先作出可行域，再作出直线l0：y=2x，将l0平移与可行域有公共点，直线y=2x-z在y轴上的截距最小时，z有最大值，求出此时直线y=2x-z经过的可行域内的点的坐标，代入z=2x-y中即可．
    解答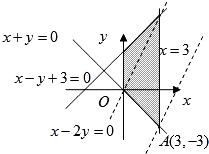：精英家教网解：如图，作出可行域，作出直线l0：y=2x，将l0平移至过点A处时，函数z=2x-y有最大值9．
    故选D
    点评：本题考查线性规划问题，考查数形结合思想，解答的步骤是有两种方法：一种是：画出可行域画法，标明函数几何意义，得出最优解．另一种方法是：由约束条件画出可行域，求出可行域各个角点的坐标，将坐标逐一代入目标函数，验证，求出最优解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若实数x，y满足约束条件
    x+2y≥3
    2x+y≤3
    ，且x≥0，则x-y的最大值为
    0
    0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若实数x，y满足约束条件
    5x+3y≤15
    y≤x+1
    x-5y≤3
    ，则z=3x+5y    的最大值为
    17
    17
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若实数x，y满足约束条件
    x+1≥0
    x-y+1≤0
    x+y-2≤0
    ，则z=4x+y的最大值为
    7
    2
    7
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若实数x，y满足约束条件
    x+y≥0
    y≤x+2
    0≤x≤1
    ，则z=2x-y的最小值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•黄浦区二模）若实数x、y满足约束条件
    x≥0
    y≥0
    2x+y-24≤0
    -3x+y+6≥0
    则目标函数z=2x-3y的最小值是（　　）

    查看答案和解析>>

    同步练习册答案