
【题目】如图,已知底角为![]() 的等腰梯形
的等腰梯形![]() ,底边
,底边![]() 长为12,腰长为
长为12,腰长为![]() ,当一条垂直于底边
,当一条垂直于底边![]() (垂足为
(垂足为![]() )的直线
)的直线![]() 从左至右移动(与梯形
从左至右移动(与梯形![]() 有公共点)时,直线
有公共点)时,直线![]() 把梯形分成两部分.
把梯形分成两部分.
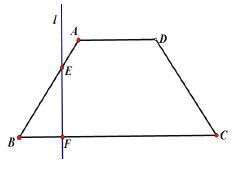
(1)令![]() ,试写出直线右边部分的面积
,试写出直线右边部分的面积![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)在(1)的条件下,令![]() .构造函数
.构造函数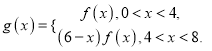
①判断函数![]() 在
在![]() 上的单调性;
上的单调性;
②判断函数![]() 在定义域内是否具有单调性,并说明理由.
在定义域内是否具有单调性,并说明理由.
【答案】(1)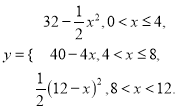 ;(2)见解析.
;(2)见解析.
【解析】试题分析:首先根据题意寻求y 与自变量x的关系,根据x的不同情况求出y与x的函数关系,得出分段函数;根据所求出的函数f(x)的解析式,按照函数g(x)的要求,写出对应的函数g(x)的解析式,研究函数g(x)在(4,8)的单调性,按照分段函数的解析式分段研究函数的单调性.
试题解析:
(1)过点![]() 分别作
分别作![]() ,垂足分别是
,垂足分别是![]() .因为等腰梯形
.因为等腰梯形![]() 的底角为
的底角为![]() ,腰长为
,腰长为![]() ,所以
,所以![]() ,又
,又![]() ,所以
,所以![]() .
.
![]() 当点
当点![]() 在
在![]() 上时,即
上时,即![]() 时,
时, ![]() ;
;
![]() 当点
当点![]() 在
在![]() 上时,即
上时,即![]() 时,
时, ![]() ;
;
![]() 当点
当点![]() 在
在![]() 上时,即
上时,即![]() 时,
时, ![]() .
.
所以,函数解析式为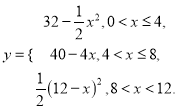
(2)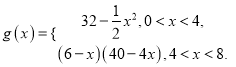
① 由二次函数的性质可知,函数![]() 在
在![]() 上是减函数.
上是减函数.
② 虽然![]() 在
在![]() 和
和![]() 单调递减,
单调递减,
但是![]() ,∴
,∴![]() .
.
因此函数![]() 在定义域内不具有单调性.
在定义域内不具有单调性.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
【题目】某渔场有一边长为20m的正三角形湖面ABC(如图所示),计划筑一条笔直的堤坝DE将水面分成面积相等的两部分,以便进行两类水产品养殖试验(D在AB上,E在AC上).

(1)为了节约开支,堤坝应尽可能短,请问该如何设计?堤坝最短为多少?
(2)将DE设计为景观路线,堤坝应尽可能长,请问又该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网络购物已经成为一种时尚,电商们为了提升知名度,加大了在媒体上的广告投入.经统计,近五年某电商在媒体上的广告投入费用x(亿元)与当年度该电商的销售收入y(亿元)的数据如下表:):
年份 | 2012年 | 2013年 | 2014 | 2015 | 2016 |
广告投入x | 0.8 | 0.9 | 1 | 1.1 | 1.2 |
销售收入y | 16 | 23 | 25 | 26 | 30 |
(1)求y关于x的回归方程; (2)2017年度该电商准备投入广告费1.5亿元,
利用(1)中的回归方程,预测该电商2017年的销售收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为: 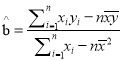
![]() ,选用数据:
,选用数据: ![]() ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作抛物线
作抛物线![]() 的两条切线, 切点分别为
的两条切线, 切点分别为![]() ,
, ![]() .
.
(1) 证明: ![]() 为定值;
为定值;
(2) 记△![]() 的外接圆的圆心为点
的外接圆的圆心为点![]() , 点
, 点![]() 是抛物线
是抛物线![]() 的焦点, 对任意实数
的焦点, 对任意实数![]() , 试判断以
, 试判断以![]() 为直径的圆是否恒过点
为直径的圆是否恒过点![]() ? 并说明理由.
? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放k(1≤k≤4,且k∈R)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=k·f(x),其中f(x)=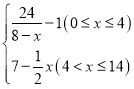 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值;
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
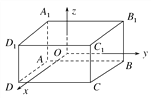
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com