
在空间四边形ABCD中,已知AD=1,BC=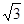 ,且AD⊥BC,对角线BD=
,且AD⊥BC,对角线BD= ,AC=
,AC= , AC和BD所成的角是( )
, AC和BD所成的角是( )
A. | B. | C. | D. |
C
解析试题分析: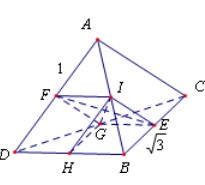
分别取BC、AD、CD、BD、AB中点E、F、G、H、I,
连接EF、EG、EI、FG、FI、GH、GI、HI
∵△BCD中,GE是中位线,∴GE∥BD且GE=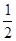 BD
BD
同理可得FI∥BD且FI=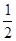 BD
BD
∴GE∥FI且GE=FI,得四边形EGFI是平行四边形
∵FG∥AC,GE∥BD
∴∠FGE(或其补角)是异面直线AC和BD所成的角
同理可得∠GHI(或其补角)是异面直线AD和BC所成的角
∵AD⊥BC,∴∠GHI=90°
∵GH=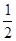 BC=
BC=  ,HI=
,HI=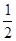 AD=
AD=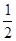 ,∴GI=" GH2+HI2" =1
,∴GI=" GH2+HI2" =1
∵平行四边形EGFI中,FI=GE=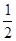 BD=
BD=  ,FG=EI=
,FG=EI=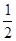 AC=
AC=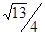
∴ ,得
,得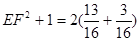 ,解得EF=1
,解得EF=1
因此,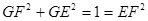 ,可得∠FGE=
,可得∠FGE=
∴异面直线AC和BD所成的角为
考点:异面直线及其所成的角.
点评:本题在空间四边形ABCD中,已知相对棱的长度和所成角,并且知道对角线长度的情况下求对角线
所成角大小,着重考查了空间四边形的性质和异面直线所成角求法等知识,属于中档题.


科目:高中数学 来源: 题型:单选题
在空间四边形ABCD中,在AB、BC、DC、DA上分别取E、F、G、H四点,如果GH、EF交于一点P,则 ( )
A.P一定在直线BD上
B.P一定在直线AC上
C.P在直线AC或BD上
D.P既不在直线BD上,也不在AC上
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知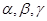 是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①
是三个不重合的平面,a,b是两条不重合的直线,有下列三个条件:①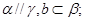 ②
②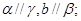 ③
③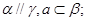 如果命题
如果命题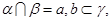 且_______,则
且_______,则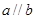 为真命题,则可以在横线处填入的条件是( )
为真命题,则可以在横线处填入的条件是( )
| A.①或② | B.②或③ | C.①或③ | D.只有② |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设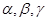 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
①若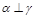 ,
,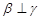 ,则
,则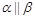 ;
;
②若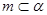 ,
,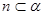 ,
,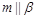 ,
,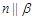 ,则
,则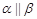 ;
;
③若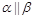 ,
,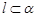 ,则
,则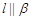 ;
;
④若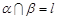 ,
,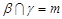 ,
,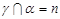 ,
,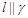 ,则
,则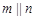 其中真命
其中真命
题的个数是 ( )))
| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知直线 a和平面?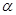 ,
,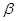 ,
,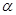 ∩
∩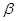 =l,a
=l,a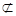
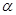 ,a
,a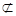
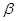 ,a在
,a在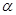 ,
,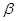 内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
内的射影分别为直线 b 和 c ,则 b 和 c 的位置关系是( )
| A.相交或平行 | B.相交或异面 |
| C.平行或异面 | D.相交﹑平行或异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设 是三个不重合的平面,l是直线,给出下列命题:
是三个不重合的平面,l是直线,给出下列命题:
①若 ,则
,则 ; ②若
; ②若
③若l上存在两点到 的距离相等,则
的距离相等,则 ; ④若
; ④若
其中正确的命题是( )
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com