
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,椭圆
,椭圆![]() 上一点
上一点![]() 到
到![]() 的距离之和为4.过点
的距离之和为4.过点![]() 作直线
作直线![]() 的垂线
的垂线![]() 交直线
交直线![]() 于点
于点![]() .
.
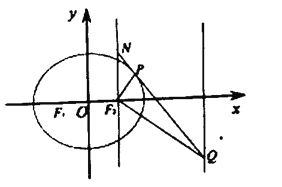
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)试判断直线![]() 与椭圆
与椭圆![]() 公共点的个数,并说明理由;
公共点的个数,并说明理由;
(3)直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .(2)答案见解析.(3)
.(2)答案见解析.(3)![]()
【解析】
(1)根据题意,可得出![]() ,已知条件结合椭圆的定义得
,已知条件结合椭圆的定义得![]() ,再由
,再由![]() 求出
求出![]() ,即可得到椭圆的方程;
,即可得到椭圆的方程;
(2)设![]() ,
,![]() ,直线
,直线![]() 的方程从而得出
的方程从而得出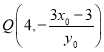 ,求出
,求出![]() 的方程,与椭圆联立解方程求解,即可判断出直线
的方程,与椭圆联立解方程求解,即可判断出直线![]() 与椭圆
与椭圆![]() 公共点的个数;
公共点的个数;
(3)由(2)知,直线![]() 的方程为:
的方程为:![]() ,与直线
,与直线![]() 交于点
交于点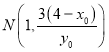 ,运用两点间距离公式,可分别求出
,运用两点间距离公式,可分别求出![]() 和
和![]() ,从而得出
,从而得出![]() 的值.
的值.
(1)设椭圆的焦距为![]() ,
,
因为![]() ,
,![]() 为椭圆的左右焦点,所以
为椭圆的左右焦点,所以![]() ,
,
因为点![]() 到
到![]() 的距离之和为4,所以
的距离之和为4,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
所以,椭圆![]() 的标准方程
的标准方程![]() .
.
(2)设![]() ,
,![]() ,由点
,由点![]() 在椭圆
在椭圆![]() 上得
上得![]() ,
,
直线![]() 的方程为
的方程为![]() ,它与直线
,它与直线![]() 交于点
交于点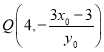 ,
,
所以,直线![]() 的方程为
的方程为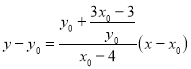 ,结合
,结合![]() ,
,
直线![]() 的方程可化为
的方程可化为![]() .
.
与椭圆![]() 联立,整理得
联立,整理得![]() ,解得
,解得![]() .
.
所以直线![]() 与椭圆
与椭圆![]() 只有一个公共点
只有一个公共点![]() .
.
(3)由(2)知,直线![]() 的方程为:
的方程为:![]() ,
,
它与直线![]() 交于点
交于点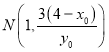 ,则
,则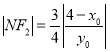 ,
,
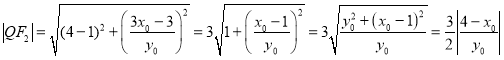 ,
,
所以,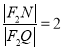 .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程选讲
在平面直角坐标系中,以原点为极点,以![]() 轴非负半轴为极轴建立极坐标系, 已知曲线
轴非负半轴为极轴建立极坐标系, 已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线![]() 过点
过点![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的焦距为
的焦距为![]() ,斜率为
,斜率为![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点,若线段
两点,若线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 的斜率为
的斜率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若过左焦点![]() 斜率为
斜率为![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]()
![]() 为椭圆上一点,且满足
为椭圆上一点,且满足![]() ,问:
,问:![]() 是否为定值?若是,求出此定值,若不是,说明理由.
是否为定值?若是,求出此定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
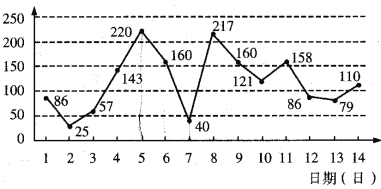
【题目】下图是某市2月1日至14日的空气质量指数趋势图及空气质量指数与污染程度对应表.某人随机选择2月1日至2月13日中的某一天到该市出差,第二天返回(往返共两天).
空气质量指数 | 污染程度 |
小于100 | 优良 |
大于100且小于150 | 轻度 |
大于150且小于200 | 中度 |
大于200且小于300 | 重度 |
(1)由图判断从哪天开始连续三天的空气质量指数方差最大?(只写出结论不要求证明)
(2)求此人到达当日空气质量优良的概率;
(3)求此人出差期间(两天)空气质量至少有一天为中度或重度污染的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月25日-27日,北京召开第二届“一带一路”国际高峰论坛,组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问,要求这三个媒体团中既有国内媒体团又有国外媒体团,且国内媒体团不能连续提问,则不同的提问方式的种数为 ( )
A. 198B. 268C. 306D. 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com