
【题目】设{an}是公比大于1的等比数列,Sn为数列{an}的前n项和,已知S3=7,
且a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项;
(2)令![]() ,n=1,2,…,求数列{bn}的前n项和Tn .
,n=1,2,…,求数列{bn}的前n项和Tn .
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的各项均为正数,a1=1,前n项和为Sn , 且an+12﹣nλ2﹣1=2λSn , λ为正常数.
(1)求数列{an}的通项公式;
(2)记bn= ![]() ,Cn=
,Cn= ![]() +
+ ![]() (k,n∈N*,k≥2n+2). 求证:
(k,n∈N*,k≥2n+2). 求证:
①bn<bn+1;
②Cn>Cn+1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点. 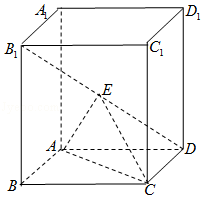
(Ⅰ)证明:平面ACE⊥平面ABCD;
(Ⅱ)若二面角D﹣AE﹣C为60°,AA1=AB=1,求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() 的圆心为
的圆心为 ![]() 的圆心为N,一动圆与圆M内切,与圆N外切.
的圆心为N,一动圆与圆M内切,与圆N外切.
(1)求动圆圆心P的轨方迹方程;
(2)设A,B分别为曲线P与x轴的左右两个交点,过点 ![]() 的直线
的直线 ![]() 与曲线P交于C,D两点,若
与曲线P交于C,D两点,若 ![]() ,求直线
,求直线 ![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com