练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在空间四边形ABCD中，点E，H分别是边AB，AD的中点，点F，G分别是边BC，CD上的点，且，则下列说法正确的是________．(填写所有正确说法的序号)

    ①EF与GH平行； ②EF与GH异面；

    ③EF与GH的交点M可能在直线AC上，也可能不在直线AC上；

    ④EF与GH的交点M一定在直线AC上．

    【答案】④.

    【解析】分析：由题意结合空间几何体的结构特征和立体几何公理逐一考查所给命题的真假即可.

    详解：E，H分别是边AB，AD的中点，则，且,

    F，G分别是边BC，CD上的点，且，

    则，且,

    据此可得四边形是梯形，且，

    据此可知：EF与GH不平行；EF与GH共面；

    直线在平面内，直线在平面内，

    则直线EF与GH的交点M一定在平面与平面的交线直线AC上．

    综上可得，题中所给的说法正确的是④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知动点到定点的距离和它到直线的距离的比值为常数，记动点的轨迹为曲线.

    (1)求曲线的方程；

    (2)若直线与曲线相交于不同的两点， ，直线与曲线相交于不同的两点 ，且，求以， ， ， 为顶点的凸四边形的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）= sin2x﹣cos2x﹣ ，（x∈R）．
    （1）求函数f（x）的最小值和最小正周期；
    （2）设△ABC的内角A、B、C的对边分别为a、b、c，且c= ，f（C）=0，若 =（1，sinA）与 =（2，sinB）共线，求a，b的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P-ABCD中，AD∥BC，ADC=PAB=90°，BC=CD=AD.E为棱AD的中点，异面直线PA与CD所成的角为90°.

    （I）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；

    (II)若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平行六面体中，．

    求证：（1）；

    （2）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线关于轴对称，顶点在坐标原点，直线经过抛物线的焦点.

    (1)求抛物线的标准方程；

    (2)若不经过坐标原点的直线与抛物线相交于不同的两点， ，且满足，证明直线过轴上一定点，并求出点的坐标.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在正方体中，是上一点，是的中点，平面

    （Ⅰ）求证：平面；

    （Ⅱ）求与平面所成的角

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数=lnx+ax2+(2a+1)x．

    （1）讨论的单调性；

    （2）当a﹤0时，证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】x的取值范围为[0，10]，给出如图所示程序框图，输入一个数x．
    （1）请写出程序框图所表示的函数表达式；
    （2）求输出的y（y＜5）的概率；
    （3）求输出的y（6＜y≤8）的概率．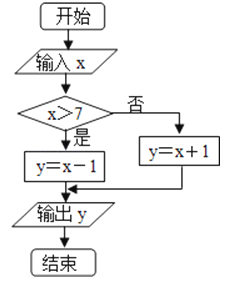

    查看答案和解析>>

    同步练习册答案