练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】选修4-4：坐标系与参数方程

    已知直线的参数方程为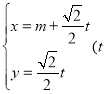为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．且曲线的左焦点在直线上．

    （1）若直线与曲线交于两点，求的值；

    （2）求曲线的内接矩形的周长的最大值．

    【答案】（1）；（2）．

    【解析】

    试题分析：（1）首先求出曲线的普通方程和焦点坐标, 然后将直线的参数方程代入曲线的普通方程, 利用根与系数的关系和参数的几何意义, 即可得到结果；（2）首先根据椭圆参数方程设出动点的坐标, 然后将矩形周长用三角函数表示出, 再利用三角函数的有界性求解 ．

    试题解析：（1）已知曲线的标准方程为 ，则其左焦点为，则，将直线的参数方程与曲线的方程 联立，得，则．

    （2）由曲线的方程为 ，可设曲线上的动点，则以为顶点的内接矩形周长为，因此该内接矩形周长的最大值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)＝ax＋x2－xlna，a>1.

    (1)求证：函数f(x)在(0，＋∞)上单调递增；

    (2)对任意x1，x2∈[－1,1]，|f(x1)－f(x2)|≤e－1恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】用0，1，2， 3，4，5这六个数字：

    （1）能组成多少个无重复数字的四位偶数？

    （2）能组成多少个无重复数字且为5的倍数的五位数？

    （3）能组成多少个无重复数字且比1325大的四位数？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图几何体是四棱锥，为正三角形， ，且.

    （1）求证: 平面平面；

    （2）是棱的中点，求证:平面；

    （3）求二面角的平面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数， ， 为自然对数的底数.

    （Ⅰ）若函数存在两个零点，求的取值范围；

    （Ⅱ）若对任意， ， 恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】新一届班委会的7名成员有、、三人是上一届的成员，现对7名成员进行如下分工.

    （Ⅰ）若正、副班长两职只能由、、三人选两人担任，则有多少种分工方案？

    （Ⅱ）若、、三人不能再担任上一届各自的职务，则有多少种分工方案？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中实数．

    （1）若，求函数在上的最值；

    （2）若，讨论函数的单调性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，函数．

    （1）若，求曲线在处的切线方程；

    （2）若无零点，求实数的取值范围；

    （3）若有两个相异零点，，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的短轴长为，离心率．

    （1）求椭圆的标准方程；

    （2）若分别是椭圆的左、右焦点，过的直线与椭圆交于不同的两点，求的内切圆半径的最大值.

    查看答案和解析>>

    同步练习册答案