
【题目】设数列{an}满足:a1=1,an+1=3an , n∈N* . 设Sn为数列{bn}的前n项和,已知b1≠0,2bn﹣b1=S1Sn , n∈N*(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=bnlog3an , 求数列{cn}的前n项和Tn .
【答案】解:(Ⅰ)∵an+1=3an , ∴{an}是公比为3,首项a1=1的等比数列, ∴通项公式为an=3n﹣1 .
∵2bn﹣b1=S1Sn , ∴当n=1时,2b1﹣b1=S1S1 ,
∵S1=b1 , b1≠0,∴b1=1.
∴当n>1时,bn=Sn﹣Sn﹣1=2bn﹣2bn﹣1 , ∴bn=2bn﹣1 ,
∴{bn}是公比为2,首项a1=1的等比数列,
∴通项公式为bn=2n﹣1 .
(Ⅱ)cn=bnlog3an=2n﹣1log33n﹣1=(n﹣1)2n﹣1 ,
Tn=020+121+222+…+(n﹣2)2n﹣2+(n﹣1)2n﹣1…①
2Tn=021+122+223+…+(n﹣2)2n﹣1+(n﹣1)2n…②
①﹣②得:﹣Tn=020+21+22+23+…+2n﹣1﹣(n﹣1)2n
=2n﹣2﹣(n﹣1)2n=﹣2﹣(n﹣2)2n
∴Tn=(n﹣2)2n+2.
【解析】(Ⅰ)判断an}是等比数列,求出通项公式,判断{bn}是等比数列,求出通项公式为bn . (Ⅱ)化简cn的表达式,利用错位相减法求解Tn即可.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系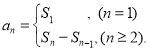 .
.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,已知![]() 是一幢6层的写字楼,每层高均为3m,在
是一幢6层的写字楼,每层高均为3m,在![]() 正前方36m处有一建筑物
正前方36m处有一建筑物![]() ,从楼顶
,从楼顶![]() 处测得建筑物
处测得建筑物![]() 的张角为
的张角为![]() .
.
(1)求建筑物![]() 的高度;
的高度;
(2)一摄影爱好者欲在写字楼![]() 的某层拍摄建筑物
的某层拍摄建筑物![]() .已知从摄影位置看景物所成张角最大时,拍摄效果最佳.问:该摄影爱好者在第几层拍摄可取得最佳效果(不计人的高度)?
.已知从摄影位置看景物所成张角最大时,拍摄效果最佳.问:该摄影爱好者在第几层拍摄可取得最佳效果(不计人的高度)?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+b(a>0,a≠1)满足f(x+y)=f(x)f(y),且f(3)=8.
(1)求实数a,b的值;
(2)若不等式|x﹣1|<m的解集为(b,a),求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是 ( )
①“x=![]() ”是“
”是“![]() ”的充分不必要条件;
”的充分不必要条件;
②若a>b,则am2>bm2;
③命题“x∈R,sinx≤1”的否定是“x∈R,sinx>1”;
④函数f(x)=![]() -cosx在[0,+∞)内有且仅有两个零点.
-cosx在[0,+∞)内有且仅有两个零点.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本为
千件,需另投入成本为![]() 万元,当年产量不足80千件时,
万元,当年产量不足80千件时, ![]() (万元);当年产量不少于80千件时,
(万元);当年产量不少于80千件时, ![]() (万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(万元).通过市场分析,若每件售价为500元时,该厂年内生产的商品能全部销售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
点击量 |
|
|
|
节数 | 6 | 18 | 12 |
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间![]() 内,则需要花费40分钟进行剪辑,若点击量在区间
内,则需要花费40分钟进行剪辑,若点击量在区间![]() 内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间
内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在公比为正数的等比数列{an}中, ![]() ,
, ![]() ,数列{bn}(bn>0)的前n项和为Sn满足
,数列{bn}(bn>0)的前n项和为Sn满足 ![]() (n≥2),且S10=100.
(n≥2),且S10=100.
( I)求数列{an}和数列{bn}的通项公式;
( II)求数列{anbn}的前n项和为Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 上的点到二定点
上的点到二定点![]() 、
、![]()
![]() 的距离之和为定值
的距离之和为定值![]() ,以
,以![]() 为圆心半径为4的圆
为圆心半径为4的圆![]() 与
与![]() 有两交点,其中一交点为
有两交点,其中一交点为![]() ,
, ![]() 在y轴正半轴上,圆
在y轴正半轴上,圆![]() 与x轴从左至右交于
与x轴从左至右交于![]() 二点,
二点, ![]() .
.
(1)求曲线![]() 、
、![]() 的方程;
的方程;
(2)曲线![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,过
,过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 交于
交于![]() 二点,过
二点,过![]() 做
做![]() 的切线
的切线![]() ,
, ![]() 交于
交于![]() .当
.当![]() 在x轴上方时,是否存在点
在x轴上方时,是否存在点![]() ,满足
,满足![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com