
【题目】在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1类比到空间,在长方体中,一条对角线与从其一顶点出发的三个面所成的角分别为α,β,γ,则有cos2α+cos2β+cos2γ= .
【答案】2
【解析】解:我们将平面中的两维性质,类比推断到空间中的三维性质.
由在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1,
我们根据长方体性质可以类比推断出空间性质,
∵长方体ABCD﹣A1B1C1D1中,如图
对角线AC1与过A点的三个面ABCD,AA1B1B、AA1D1D所成的角分别为α,β,γ,
∴cosα= ![]() ,cosβ=
,cosβ= ![]() ,cosγ=
,cosγ= ![]() ,
,
令同一顶点出发的三个棱的长分别为a,b,c,则有cos2α+cos2β+cos2γ= ![]() =2
=2
所以答案是:2.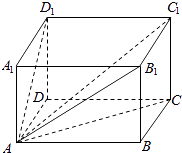
【考点精析】本题主要考查了类比推理的相关知识点,需要掌握根据两类不同事物之间具有某些类似(或一致)性,推测其中一类事物具有与另外一类事物类似的性质的推理,叫做类比推理才能正确解答此题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160)、第二组[160,165);…第八组[190,195],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.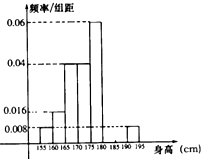
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
(2)求第六组、第七组的频率并补充完整频率分布直方图;
(3)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为x、y,求满足|x﹣y|≤5的事件概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R). 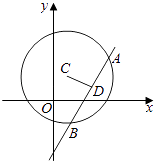
(1)求证:无论m取什么实数,直线l恒过第一象限;
(2)求直线l被圆C截得的弦长最短时m的值以及最短长度;
(3)设直线l与圆C相交于A、B两点,求AB中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,且对任意x1 , x2∈(0,+∞)都有 ![]() <0(x1≠x2),若实数a满足f(log3a﹣1)+2f(
<0(x1≠x2),若实数a满足f(log3a﹣1)+2f( ![]() a)≥3f(1),则a的取值范围是( )
a)≥3f(1),则a的取值范围是( )
A.[ ![]() ,3]
,3]
B.[1,3]
C.(0, ![]() )
)
D.(0,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=BB1=1,B1C=2. 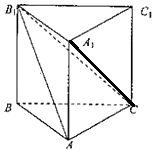
(1)求证:平面B1AC⊥平面ABB1A1;
(2)求直线A1C与平面B1AC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴上的圆
轴上的圆![]() 与直线
与直线![]() 切于点
切于点![]() .
.
(1)求圆![]() 的标准方程;
的标准方程;
(2)已知![]() ,经过原点,且斜率为正数的直线
,经过原点,且斜率为正数的直线![]() 与圆
与圆![]() 交于
交于![]() 两点.
两点.
(ⅰ)求证: ![]() 为定值;
为定值;
(ⅱ)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心为(1,1)的圆C经过点M(1,2).
(1)求圆C的方程;
(2)若直线x+y+m=0与圆C交于A、B两点,且△ABC是直角三角形,求实数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若an=log(n+1)(n+2)(n∈N),我们把使乘积a1a2…an为整数的数n叫做“劣数”,则在区间(1,2004)内所有劣数的和为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com