
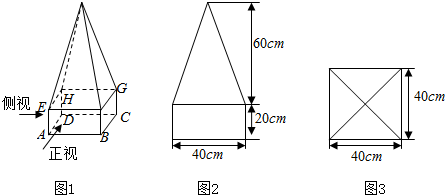
分析 (1)根据几何体的直观图以及正视图和俯视图,即可得出它的侧视图;
(2)根据图中数据即可求出该几何体的表面积.
解答 解:(1)根据题意,画出该安全标识墩的侧视图,
如图所示;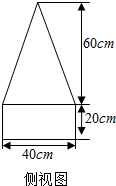
(2)∵该安全标识墩的上半部分是正四棱锥,
且底面是边长为40cm的正方形,正四棱锥的高为60cm,
∴正四棱锥的斜高为20$\sqrt{10}$,
下半部分是长、宽、高分别为40cm,40cm,20cm的长方体,
∴该安全标识墩的表面积为:
S=(20×40+$\frac{1}{2}$×40×20$\sqrt{10}$)×4+40×40=800(6+2$\sqrt{10}$)(cm2).
点评 本题考查了简单组合体的三视图与表面积的应用问题,解题的关键是准确判断空间几何体的形状,是基础题目.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-,+∞) | B. | (-1,2) | C. | {y|y≠2} | D. | {y|y>2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
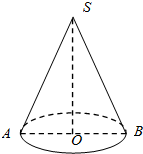 如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.
如图,在圆锥SO中,其母线长为2,底面半径为$\frac{1}{2}$,一只虫子从底面圆周上一点A出发沿圆锥表面爬行一周后又回到A点,则这只虫子所爬过的最短路程是2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 施化肥量x | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 水稻产量y | 330 | 345 | 365 | 405 | 445 | 450 | 455 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
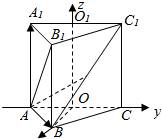 如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.
如图所示,在空间直角坐标系中有正三棱柱ABC-A1B1C1点是O、O1分别是棱AC、A1C1的中点,且AA1=$\sqrt{2}$,AB1⊥BC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com