
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 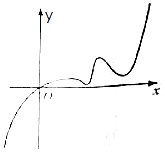
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
【答案】A
【解析】解:由图可知,当x>0时,导函数f'(x)>0,原函数单调递增, ∵两正数a,b满足f(2a+b)<2,
又由f(2)=2,即f(2a+b)<2,
即2a+b<2,
又由a>0.b>0;
故a,b所对应的平面区域如下图所示: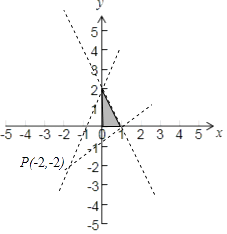
![]() 表示动点(a,b)与定点(﹣2,﹣2)连线的斜率,
表示动点(a,b)与定点(﹣2,﹣2)连线的斜率,
当直线过(1,0)点时, ![]() =
= ![]() ,
,
当直线过(0,2)点时, ![]() =2,
=2,
故 ![]() ∈(
∈( ![]() ,2),
,2),
故选:A.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
①记Qi为第i名工人在这一天中加工的零件总数,则Q1 , Q2 , Q3中最大的是 .
②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1 , p2 , p3中最大的是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴的正半轴建立平面直角坐标系,直线
轴的正半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(I)写出直线![]() 的一般方程与曲线
的一般方程与曲线![]() 的直角坐标方程,并判断它们的位置关系;
的直角坐标方程,并判断它们的位置关系;
(II)将曲线![]() 向左平移
向左平移![]() 个单位长度,向上平移
个单位长度,向上平移![]() 个单位长度,得到曲线
个单位长度,得到曲线![]() ,设曲线
,设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,设曲线
,设曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市要对该市六年级学生进行体育素质调查测试,现让学生从“跳绳、短跑![]() 米、长跑
米、长跑![]() 米、仰卧起坐、游泳
米、仰卧起坐、游泳![]() 米、立定跳远”
米、立定跳远”![]() 项中选择
项中选择![]() 项进行测试,其中“短跑、长跑、仰卧起坐”
项进行测试,其中“短跑、长跑、仰卧起坐”![]() 项中至少选择其中
项中至少选择其中![]() 项进行测试.现从该市六年级学生中随机抽取了
项进行测试.现从该市六年级学生中随机抽取了![]() 名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中
名学生进行调查,他们选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数及人数统计如下表:(其中![]() )
)
选择的项目中包含“短跑、长跑、仰卧起坐”的项目个数 |
|
|
|
人数 |
|
|
|
已知从所调查的![]() 名学生中任选
名学生中任选![]() 名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为
名,他们选择“短跑、长跑、仰卧起坐”的项目个数不相等概率为![]() ,记
,记![]() 为这
为这![]() 名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
名学生选择“短跑、长跑、仰卧起坐”的项目个数之和.
(1)求![]() 的值;
的值;
(2)求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子500米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造中国男子冰上竞速项目在冬奥会金牌零的突破.某高校为调查该校学生在冬奥会期间累计观看冬奥会的时间情况,收集了200位男生、100位女生累计观看冬奥会时间的样本数据(单位:小时).又在100位女生中随机抽取20个人,已知这20位女生的数据茎叶图如图所示.
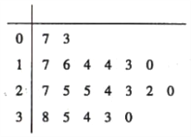

(I)将这20位女生的时间数据分成8组,分组区间分别为![]()
![]() ,
,![]() ,…,
,…,![]() ,
,![]()
![]() ,完成频率分布直方图;
,完成频率分布直方图;
(II)以(I)中的频率作为概率,求1名女生观看冬奥会时间不少于30小时的概率;(III)以(I)中的频率估计100位女生中累计观看时间小于20个小时的人数,已知200位男生中累计观看时间小于20小时的男生有50人.请完成下面的列联表,并判断是否有99%的把握认为“该校学生观看冬奥会累计时间与性别有关”.
男生 | 女生 |
| |
累计观看时间小于20小时 | |||
累计观看时间小于20小时 | |||
总计 | 300 |
附:(![]()
![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,己知曲线C1 的方程为ρ=2cosθ+2sinθ,直线 C2 的参数方程为![]() (t 为参数)
(t 为参数)
(Ⅰ)将 C1 的方程化为直角坐标方程;
(Ⅱ)P 为 C1 上一动点,求 P 到直线 C2 的距离的最大值和最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com