
 ,三人都做对的概率是
,三人都做对的概率是 ,三人全做错的概率是
,三人全做错的概率是 ,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为
,已知乙做对这道题的概率大于丙做对这道题的概率.设三人中做对这道题的人数为 ,则随机变量
,则随机变量 的数学期望
的数学期望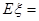 .
. 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源:不详 题型:解答题
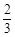 ,现种植这种种子4粒,求:
,现种植这种种子4粒,求: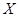 的分布列及平均数.
的分布列及平均数. 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 层下电梯的概率
层下电梯的概率 ;
; 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 中任选出两位同学,共同帮助成绩在
中任选出两位同学,共同帮助成绩在 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若 同学成绩为43分,
同学成绩为43分, 同学成绩为95分,求
同学成绩为95分,求 、
、 两同学恰好被安排在“二帮一”中同一小组的概率.
两同学恰好被安排在“二帮一”中同一小组的概率.| 分 组 | 频 数 | 频 率 |
| [40, 50 ) | 2 | 0.04 |
| [ 50, 60 ) | 3 | 0.06 |
| [ 60, 70 ) | 14 | 0.28 |
| [ 70, 80 ) | 15 | 0.30 |
| [ 80, 90 ) | | |
| [ 90, 100 ] | 4 | 0.08 |
| 合 计 | | |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
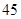 名,女同学有
名,女同学有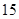 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个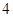 人的课外兴趣小组.
人的课外兴趣小组.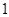 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com