
 已知三棱柱ABC-A1B1C1的各棱长都为1,M是底面上BC边的中点,N是侧棱CC1上的点,且CN=$\frac{1}{4}$CC1,求证:AB1⊥MN.
已知三棱柱ABC-A1B1C1的各棱长都为1,M是底面上BC边的中点,N是侧棱CC1上的点,且CN=$\frac{1}{4}$CC1,求证:AB1⊥MN. 分析 设AB中点为O,作OO1∥AA1,以O为原点,OB为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系,利用向量法能证明AB1⊥MN.
解答 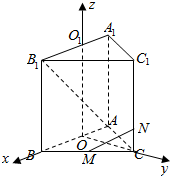 解:设AB中点为O,作OO1∥AA1,
解:设AB中点为O,作OO1∥AA1,
以O为原点,OB为x轴,OC为y轴,OO1为z轴,建立空间直角坐标系,
由已知得A(-$\frac{1}{2}$,0,0),B1($\frac{1}{2},0,1$),
B($\frac{1}{2},0,0$),C(0,$\frac{\sqrt{3}}{2}$,0),C1(0,$\frac{\sqrt{3}}{2}$,1),
M($\frac{1}{4}$,$\frac{\sqrt{3}}{4}$,0),N(0,$\frac{\sqrt{3}}{2}$,$\frac{1}{4}$),
$\overrightarrow{A{B}_{1}}$=(1,0,1),$\overrightarrow{MN}$=(-$\frac{1}{4}$,$\frac{\sqrt{3}}{4}$,$\frac{1}{4}$),
$\overrightarrow{A{B}_{1}}•\overrightarrow{MN}$=-$\frac{1}{4}+0+\frac{1}{4}$=0,
∴AB1⊥MN.
点评 本题考查异面直线垂直的证明,是中档题,解题时要认真审题,注意向量法的合理运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (0,1)∪(1,+∞) | C. | (0,1) | D. | (0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com