
分析 以D为原点,AD为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出直线BC1与平面BB1D1D所成角的余弦值.
解答 解: 以D为原点,AD为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
以D为原点,AD为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为1,
则B(1,1,0),C1(0,1,1),D(0,0,0),D1(0,0,1),
$\overrightarrow{B{C}_{1}}$=(-1,0,1),$\overrightarrow{D{D}_{1}}$=(0,0,1),$\overrightarrow{DB}$=(1,1,0),
设平面BB1D1D的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{D}_{1}}=z=0}\\{\overrightarrow{n}•\overrightarrow{DB}=x+y=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,-1,0),
设直线BC1与平面BB1D1D所成角为θ,
则sinθ=$\frac{|\overrightarrow{n}•\overrightarrow{B{C}_{1}}|}{|\overrightarrow{n}|•|\overrightarrow{B{C}_{1}}|}$=$\frac{1}{\sqrt{2}•\sqrt{2}}$=$\frac{1}{2}$,
∴cosθ=$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴直线BC1与平面BB1D1D所成角的余弦值为$\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查线面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题

| A. | $\frac{1}{3}\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AD}$ | B. | $\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}$ | C. | $-\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AD}$ | D. | $-\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
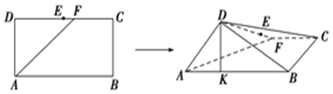 如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是( )| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{\sqrt{3}}{2}$,2) | D. | ($\frac{\sqrt{3}}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | msin2α | B. | mcos2α | C. | msinαcosα | D. | msinαtanα |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 165° | B. | 60° | C. | 25° | D. | 15° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
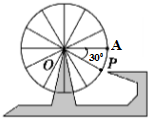 如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.
如图所示,一个半径为10m的摩天轮,轮子的底部在地面上2m处,如果此摩天轮按逆时针方向转动,每30s转一圈,且当摩天轮上某人经过点P处(∠POA=30°)时开始计时.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(1,2) | B. | (-1,0)∪(1,+∞) | C. | (0,1)∪(2,+∞) | D. | (-∞,-1)∪(0,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com