Question

【题目】在平面内将点A（2，1）绕原点按逆时针方向旋转 ，得到点B，则点B的坐标为 ．

Answer 1

【答案】（﹣ , ）
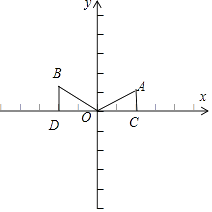
【解析】解：如图，作AC⊥x轴于C点，BD⊥x轴于D点，

∵点A的坐标为（2，1），

∴AC=1，OC=2，

∴OA= = ，

∴sin∠AOC= ，cos∠AOC= ，

∵OA绕原点按逆时针方向旋转 得OB，

∴∠AOB= ，OA=OB= ，

∴∠BOC=∠AOC+ ，

∴sin∠BOC=sin（∠AOC+ ）=sin∠AOCcos +cos∠AOCsin = ×（﹣ ）+ × = ，

cos∠BOC=cos（∠AOC+ ）=cos∠AOCcos ﹣sin∠AOCsin = ×（﹣ ）﹣ × =﹣ ，

∴DB=OBsin∠BOC= × = ，OD=OBcos∠BOC= ×（﹣ ）=﹣ ，

∴B点坐标为：（﹣ ， ）．

所以答案是：（﹣ ， ）．

【考点精析】利用两角和与差的余弦公式对题目进行判断即可得到答案，需要熟知两角和与差的余弦公式：．