
分析 由题意得购买5袋该食品可能收集到的卡片的不同结果有35种,其中能获奖的结果仅有两类,第一类:5张卡片中有3张相同的卡片,另两张各不相同;第二类:5张卡片中某两张卡片相同,而另一张是余下的另一种.由此能求出张明购买了5袋该食品,他可能获奖的概率.
解答 解:由题意得购买5袋该食品可能收集到的卡片的不同结果有35种,
其中能获奖的结果仅有两类,
第一类:5张卡片中有3张相同的卡片,另两张各不相同,这样的结果有$3{C}_{5}^{3}$${C}_{2}^{1}{C}_{1}^{1}$=60种,
第二类:5张卡片中某两张卡片相同,而另一张是余下的另一种,这样的结果有$3{C}_{5}^{2}{C}_{3}^{2}{C}_{1}^{1}$=90种,
∴张明购买了5袋该食品,他可能获奖的概率:p=$\frac{60+90}{{3}^{5}}$=$\frac{50}{81}$.
故答案为:$\frac{50}{81}$.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{e}$ | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{{e}^{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
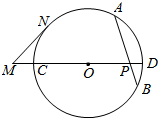 如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.
如图,⊙O中的弦AB与直径CD相交于点P,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,求MN的长.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 类别 | 1号广告 | 2号广告 | 3号广告 | 4号广告 |
| 广告次数 | 20 | 30 | 40 | 10 |
| 时间t(分钟/人) | 2 | 3 | 4 | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com