练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

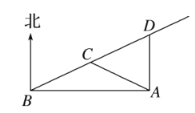
    【题目】为保障公平性，高考时每个考点都要安装手机屏蔽仪，要求在考点周围1千米处不能收到手机信号，如图，检查员抽查某市一考点，以考点正西千米的处开始为检查起点，沿着一条北偏东方向的公路，以每小时12千米的速度行驶，并用手机接通电话，问从起点开始计时，最长经过多少分钟检查员开始收不到信号（点开始），并至少持续多长时间（之间）该考点才算检查合格？

    【答案】最长经过5分钟检查员开始收不到信号，并持续至少5分钟才算检查合格

    【解析】

    根据题意，，在中通过正弦定理求得，进而，得到.得出为等边三角形，

    设检查员行驶到公路上两点之间时收不到信号，

    即公路上两点到考点的距离为1千米.

    在中，千米，千米，

    由正弦定理，得，

    （不合题意），

    ，.

    在中，千米，，

    为等边三角形，千米.

    ，在上需5分钟，上需5分钟.

    最长经过5分钟检查员开始收不到信号，并持续至少5分钟才算检查合格.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，平面ABC，，E是BC的中点，．

    求异面直线AE与所成的角的大小；

    若G为中点，求二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列四个命题：①若直线，那么直线必平行于平面内的无数条直线；②一个长为，宽为的矩形，其直观图的面积为；③若函数的定义域是，则的定义域是；④定义在上的函数，若，则函数的图象关于点中心对称.其中所有正确命题的编号为____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为矩形， 面， 为的中点。

    （1）证明： 平面;

    （2）设， ，三棱锥的体积 ，求A到平面PBC的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知{an}是各项均为正数的等比数列，且a1＋a2＝6，a1a2＝a3.

    (1)求数列{an}的通项公式；

    (2){bn}为各项非零的等差数列，其前n项和为Sn.已知S2n＋1＝bnbn＋1，求数列{}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司计划在办公大厅建一面长为米的玻璃幕墙.先等距安装根立柱，然后在相邻的立柱之间安装一块与立柱等高的同种规格的玻璃.一根立柱的造价为6400元，一块长为米的玻璃造价为元.假设所有立柱的粗细都忽略不计，且不考虑其他因素，记总造价为元（总造价=立柱造价+玻璃造价）.

    （1）求关于的函数关系式；

    （2）当时，怎样设计能使总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，平行四边形的周长为8，其对角线的端点，.

    （1）求动点的轨迹的方程；

    （2）已知点，记直线与曲线的另一交点为，直线，分别与直线交于点，.证明：以线段为直径的圆恒过点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在中，角的对边分别为，已知且.

    （1）求角；

    （2）求的面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）指出的周期、振幅、初相、对称轴并写出该函数的单调增区间；

    （2）说明此函数图象可由，上的图象经怎样的变换得到．

    查看答案和解析>>

    同步练习册答案