练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知数列{an}满足an+2-an=2，a1=1，a2=2，则{an}的前20项和为（　　）
    A．120B．210C．400D．440

    分析 利用所求值即为以3为首项、4为公差的等差数列{a2n-1+a2n}的前10项和，计算即得即可．

    解答 解：∵an+2-an=2，a1=1，a2=2，
    ∴奇数项构成以1为首项、2为公差的等差数列，
    偶数项构成以2为首项、2为公差的等差数列，
    ∴所求值即为以3为首项、4为公差的等差数列{a2n-1+a2n}的前10项和，
    ∴所求值为3×10+$\frac{10×（10-1）}{2}$×4=210，
    故选：B．

    点评 本题考查求数列的和，考查运算求解能力，注意解题方法的积累，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．设△ABC三个内角A、B、C所对的边分别为a、b、c，已知C=$\frac{π}{3}$．
    （1）若acosA=bcosB，求角A的大小；
    （2）若b=2，c=$\sqrt{3}$，求边a的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．从装有5个红球和5个黑球的口袋中任取3个球，则至少有一个红球的概率是（　　）
    A．$\frac{1}{5}$B．$\frac{1}{3}$C．$\frac{1}{2}$D．$\frac{11}{12}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

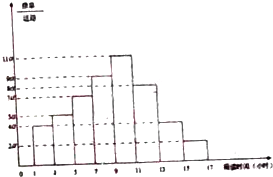    19．某所高中为了调查本校高一年级学生一周内课外阅读的投入时间（单位：小时）的情况，学校教务处对该校高一1500名在校生进行了随机编号，从0001号到1500号，抽取编号最后一位数字为3的150名学生进行问卷调查，搜集得到了这150名学生一周课外阅读时间的数据，将数据分成8个组，分组区间为：[1，3），[3，5），[5，7），…，[13，15），[15，17]，其频率分布直方图如图：
    （Ⅰ）该校问卷调查环节抽取样本过程中，运用了哪种抽样方法；
    （Ⅱ）求频率分布直方图中a的值；并求落在区间[9，11）中的学生人数b；
    （Ⅲ）根据频率分布直方图，估计本校高一年级学生周课外阅读时间的平均数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

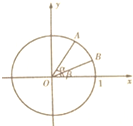    6．如图，在平面直角坐标系xOy中，以Ox轴为始边作两个锐角α，β，它们的终边分别与单位圆相交于A、B两点，已知A、B的横坐标分别为$\frac{5}{13}，\frac{3}{5}$，则tan（α+β）的值为-$\frac{56}{33}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），ab=2$\sqrt{3}$，离心率为$\frac{\sqrt{6}}{3}$．
    （Ⅰ）求椭圆的方程；
    （Ⅱ）过椭圆的右焦点F作斜率为k的直线l交椭圆于A、B两点，P为直线x=3上的一点，若△ABP为等边三角形，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知α，β为锐角，sinα=$\frac{1}{7}$，cos（α+β）=$\frac{3}{5}$．
    （Ⅰ）求sin（α+$\frac{π}{6}$）的值；
    （Ⅱ）求cosβ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．（B题）设函数f（x）=$\frac{1-sinx}{x}$，x$∈（0，\frac{π}{2}）$，则f（x）的单调性是（　　）
    A．增函数B．减函数C．先增后减函数D．先减后增函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

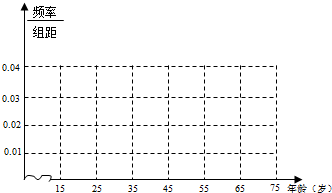
    5．某市为缓解春运期间的交通压力，计划在某路段实施“交通限行”，为了解公众对该路段“交通限行”的态度，某机构从经过该路段的人员随机抽查了50人进行调查，将调查情况进行整理，制成下表：
    年龄（岁）[15，25）[25，35）[35，45）[45，55）[55，65）[65，75]
    频数510151055
    赞成人数489643
    （1）完成被调查人员的频率分布直方图；
    （2）若从年龄在[65，75]的被调查者中随机选取2人进行进一步的采访，求选中的2人中恰好有1人赞成该路段“交通限行”的概率．

    查看答案和解析>>

    同步练习册答案