
【题目】把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.15),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65],并绘制出频率分布直方图,如图所示是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04,0.10,0.14,0.28,0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.

(1)求这次铅球投掷成绩合格的人数;
(2)你认为这次铅球投掷的同学的成绩的中位数在第几组?请说明理由;
(3)若参加这次铅球投掷的学生中,有5人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加相关部门组织的经验交流会,已知a、b 两位同学的成绩均为优秀,求a、b 两位同学中至少有1人被选到的概率.
【答案】(1)36(2)4(3)![]()
【解析】
(1)由频率之和为1,求出最后一组的频率,进而求出总人数,即可由频率求出合格人数;
(2)计算各组人数,计算出中间的人在第几组即可;
(3)给5个人分别编号,列出所有可能情况与事件所包含的情况,由古典概型计算公式计算即可.
(1)∵第6小组的频率为1-(0.04+0.10+0.14+0.28+0.30)=0.14.
∴参加这次铅球投掷的总人数为![]() =50.
=50.
根据规定,第4、5、6组的成绩均为合格,人数为(0.28+0.30+0.14)×50=36.
(2)∵成绩在第1、2、3组的人数为(0.04+0.10+0.14)×50=14,
成绩在第5、6组的人数为(0.30+0.14)×50=22,
参加这次铅球投掷的总人数为50,
∴这次铅球投掷的同学的成绩的中位数在[7.95,8.85)内,即第4组.
(3)设这次铅球投掷成绩优秀的5人分别为a、b、c、d、e,则选出2人的所有可能的情况为:ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种,
其中a、b至少有1人的情况为:ab,ac,ad,ae,bc,bd,be,共有7种,
∴a、b 两位同学中至少有1人被选到的概率为P=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,边长为4的正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( ) 参考数据: ![]() ,sin15°≈0.2588,sin7.5°≈0.1305.
,sin15°≈0.2588,sin7.5°≈0.1305.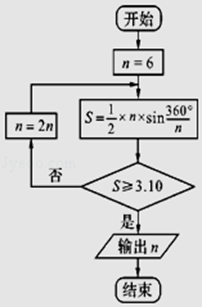
A.12
B.24
C.48
D.96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华中师大附中中科教处为了研究高一学生对物理和数学的学习是否与性别有关,从高一年级抽取60名同学(男同学30名,女同学30名),给所有同学物理题和数学题各一题,让每位同学自由选择一道题进行解答.选题情况如表:(单位:人)
物理题 | 数学题 | 总计 | |
男同学 | 16 | 14 | 30 |
女同学 | 8 | 22 | 20 |
总计 | 24 | 36 | 60 |
(1)在犯错误的概率不超过1%的条件下,能否判断高一学生对物理和数学的学习与性别有关?
(2)经过多次测试后发现,甲每次解答一道物理题所用的时间为5﹣8分钟,乙每次解答一道物理题所用的时间为6﹣8分钟,现甲、乙解同一道物理题,求甲比乙先解答完的概率;
(3)现从选择做物理题的8名女生中任意选取两人,对他们的解答情况进行全程研究,记甲、乙两女生被抽到的人数为X,求X的分布列和数学期望. 附表及公式:
P(K2k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,角
,角![]() 的终边经过点
的终边经过点![]() .若
.若![]() 是
是![]() 的图象上任意两点,且当
的图象上任意两点,且当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求 ![]() 或
或![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间;
上的单调递减区间;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数的对称性有如下结论:对于给定的函数![]() ,如果对于任意的
,如果对于任意的![]() 都有
都有![]() 成立
成立![]() 为常数),则函数
为常数),则函数![]() 关于点
关于点![]() 对称.
对称.
(1)用题设中的结论证明:函数![]() 关于点
关于点![]() ;
;
(2)若函数![]() 既关于点
既关于点![]() 对称,又关于点
对称,又关于点![]() 对称,且当
对称,且当![]() 时,
时,![]() ,求:①
,求:①![]() 的值;
的值;
②当![]() 时,
时,![]() 的表达式.
的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣1,0),B(1,0)为双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
=1(a>0,b>0)的左右顶点,点M在双曲线上,△ABM为等腰三角形,且顶角为120°,则该双曲线的标准方程为( )
A.x2﹣ ![]() =1
=1
B.x2﹣ ![]() =1
=1
C.x2﹣y2=1
D.x2﹣ ![]() =1
=1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生.

(1)分别求出(按程序框图正确编程运行时)输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据:
甲的频数统计表(部分)
运行次数 | 输出y=1 的频数 | 输出y=2 的频数 | 输出y=3 的频数 |
30 | 16 | 11 | 3 |
… | … | … | … |
2 000 | 967 | 783 | 250 |
乙的频数统计表(部分)
运行次数 | 输出y=1 的频数 | 输出y=2 的频数 | 输出y=3 的频数 |
30 | 13 | 13 | 4 |
… | … | … | … |
2 000 | 998 | 803 | 199 |
当n=2 000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() :
: ![]() 与椭圆
与椭圆![]() :
: ![]() 在第一象限的交点为
在第一象限的交点为![]() ,
, ![]() 为坐标原点,
为坐标原点, ![]() 为椭圆的右顶点,
为椭圆的右顶点, ![]() 的面积为
的面积为![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作直线
点作直线![]() 交
交![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() 两点,记
两点,记![]() 和
和![]() 的面积分别为
的面积分别为![]() 和
和![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com