
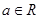 ,函数
,函数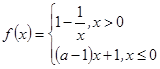 .
. 在
在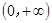 上单调递增;
上单调递增; 的零点.
的零点.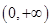 上任取两变量
上任取两变量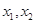 ,设
,设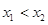 ,再对
,再对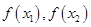 作差变形化简,判断
作差变形化简,判断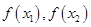 大小确定单调性.
大小确定单调性.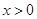 和
和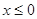 分情况求解,其中当
分情况求解,其中当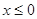 时,令
时,令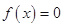 , 即
, 即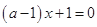 ,对此方程中参数a对根的情况进行讨论求解.
,对此方程中参数a对根的情况进行讨论求解.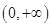 上任取两个实数
上任取两个实数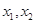 ,且
,且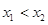 ,
,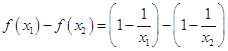

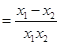 . 2分
. 2分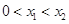 , ∴
, ∴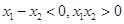 .
.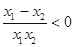 , 即
, 即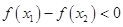 . ∴
. ∴ .
.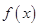 在
在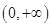 上单调递增. 4分[K]
上单调递增. 4分[K]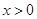 时, 令
时, 令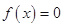 , 即
, 即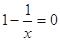 , 解得
, 解得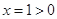 .
.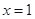 是函数
是函数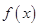 的一个零点. 6分
的一个零点. 6分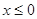 时, 令
时, 令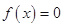 , 即
, 即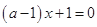 .(※)
.(※)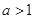 时, 由(※)得
时, 由(※)得 ,∴
,∴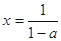 是函数
是函数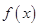 的一个零点; 8分
的一个零点; 8分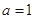 时, 方程(※)无解;
时, 方程(※)无解;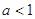 时, 由(※)得
时, 由(※)得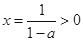 ,(不合题意,舍去) 10分
,(不合题意,舍去) 10分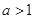 时, 函数
时, 函数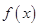 的零点是
的零点是 和
和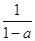 ;
; 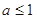 时, 函数
时, 函数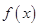 的零点是
的零点是 . 12分
. 12分

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源:不详 题型:单选题
| A.恒为正数 |
| B.恒为负数 |
| C.恒为0 |
| D.可以为正数也可以为负数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com