
分析 由题意可得离心率等于$\frac{c}{a}$=$\frac{3}{\sqrt{5}}$,设点P到右准线的距离等于|PM|,则 3|PA|+$\sqrt{5}$|PF|=3(|PA|+|PM|),故P、M、A三点共线时,|PA|+$\frac{\sqrt{5}}{3}$|PF|取得最小值,故点P的纵坐标为$\sqrt{3}$,把把y=$\sqrt{3}$代入双曲线求得正值x即为点P的横坐标.
解答 解:由题意可得双曲线$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{4}$=1的a=$\sqrt{5}$,b=2,c=3,
右焦点F(3,0),离心率等于$\frac{c}{a}$=$\frac{3}{\sqrt{5}}$,
设点P到右准线的距离等于|PM|,
则由双曲线的定义可得 $\frac{|PF|}{|PM|}$=$\frac{3}{\sqrt{5}}$,
故3|PA|+$\sqrt{5}$|PF|=3(|PA|+$\frac{\sqrt{5}}{3}$|PF|)=3(|PA|+|PM|),
当|PA|+$\frac{\sqrt{5}}{3}$|PF|取得最小值时,
P、M、A三点共线,故点P的纵坐标为$\sqrt{3}$,把y=$\sqrt{3}$代入双曲线方程,
求得正值x=$\frac{\sqrt{35}}{2}$,
故点P的坐标为($\frac{\sqrt{35}}{2}$,$\sqrt{3}$),
故答案为:($\frac{\sqrt{35}}{2}$,$\sqrt{3}$).
点评 本题考查双曲线的定义、标准方程,以及双曲线的简单性质的应用,判断P、M、A三点共线时,3PA+$\sqrt{5}$PF取得最小值,是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $(-2,\frac{6}{5})$ | B. | $[-2,\frac{6}{5})$ | C. | $[-2,\frac{6}{5}]$ | D. | $[-2,\frac{6}{5})∪\{2\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y3<y1 | C. | y3<y2<y1 | D. | y1<y3<y2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
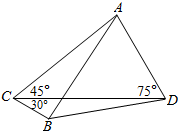 在一次抗雪救灾中,需要在A、B两地之间架设高压电线,为测量A、B两地的距离,救援人员在相距l米的C、D两地(A,B,C,D在同一平面上),测得∠ACD=45°,∠BCD=30°∠ADC=75°(如图),考虑到电线在自然下垂和施工损耗等原因,实际所得电线长度大于应是A、B距离的1.2倍,问救援至少英爱准备多长的电线?
在一次抗雪救灾中,需要在A、B两地之间架设高压电线,为测量A、B两地的距离,救援人员在相距l米的C、D两地(A,B,C,D在同一平面上),测得∠ACD=45°,∠BCD=30°∠ADC=75°(如图),考虑到电线在自然下垂和施工损耗等原因,实际所得电线长度大于应是A、B距离的1.2倍,问救援至少英爱准备多长的电线?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com