
 +1):2,求角C的大小.
+1):2,求角C的大小.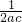 •(a2+c2-b2)=
•(a2+c2-b2)=
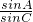 =
= =
=
 +1)sinC,2sin(120°-C)=(
+1)sinC,2sin(120°-C)=( +1)sinC
+1)sinC +1)sinC,整理得
+1)sinC,整理得 cosC=
cosC= sinC
sinC +1):2,利用正弦定理求得得
+1):2,利用正弦定理求得得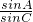 =
= 化简整理求得
化简整理求得 cosC=
cosC= sinC求得tanC的值,进而求得C.
sinC求得tanC的值,进而求得C.

科目:高中数学 来源:新课程高中数学疑难全解 题型:038
三角形三边a、b、c对应的高分别为ha、hb、hc,r为此三角形内切圆半径.若r=![]() (ha+hb+hc),试判断此三角形的形状.
(ha+hb+hc),试判断此三角形的形状.
查看答案和解析>>
科目:高中数学 来源:2011年高三数学精品复习10:定比分点、平移、正余弦定理(解析版) 题型:解答题
 +1):2,求角C的大小.
+1):2,求角C的大小.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com