(1)证明:连接A
1C,交AC
1于点O,连接OD.
由ABC-A
1B
1C
1是正三棱柱,得四边形ACC
1A
1为矩形,O为A
1C的中点.
又AD⊥BC,所以D为BC中点,所以OD为△A
1BC中位线,所以A
1B∥OD,
因为A
1B?平面ADC
1,OD?平面ADC
1,
所以A
1B∥平面ADC
1;
(2)解:过D作AC的垂线,垂足为H,过D作AC
1的垂线,垂足为N,连接NH,则∠DNH为截面ADC
1与侧面ACC
1A
1所成的二面角
∵在△ADC
1中,AD=

,DC
1=

,AC
1=2

,∴∠ADC
1=90°,∴DN=
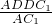
=
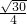
∵DH⊥AC,∴DH=

,∴NH=
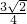
,
∴tan∠DNH=
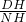
=

;
(3)解:设B
1到平面ADC
1的距离为h,则
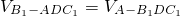
∵
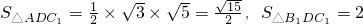
∴
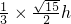
=
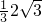
∴h=

分析:(1)连接A
1C,交AC
1于点O,连接OD,利用OD为△A
1BC中位线,可得A
1B∥OD,利用线面平行的判定,可证A
1B∥平面ADC
1;
(2)过D作AC的垂线,垂足为H,过D作AC
1的垂线,垂足为N,连接NH,则∠DNH为截面ADC
1与侧面ACC
1A
1所成的二面角,从而可求截面ADC
1与侧面ACC
1A
1所成的二面角Q-AC
1-C的正切值;
(3)设B
1到平面ADC
1的距离为h,利用
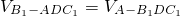
即可得到结论.
点评:本题考查线面平行,考查三棱锥体积的计算,考查面面角,掌握线面平行的判定,正确作出面面角是关键.

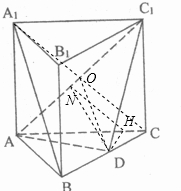
 正三棱柱ABC-A1B1C1的侧棱长和底面边长都等于2,D是BC上一点,且AD⊥BC.
正三棱柱ABC-A1B1C1的侧棱长和底面边长都等于2,D是BC上一点,且AD⊥BC.
 ,DC1=
,DC1= ,AC1=2
,AC1=2 ,∴∠ADC1=90°,∴DN=
,∴∠ADC1=90°,∴DN=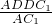 =
=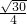
 ,∴NH=
,∴NH=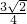 ,
,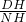 =
= ;
;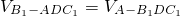
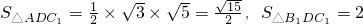
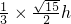 =
=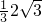

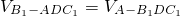 即可得到结论.
即可得到结论.

 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= 如图在 正三棱柱ABC-A1 B1 C1中,底面边长为
如图在 正三棱柱ABC-A1 B1 C1中,底面边长为 如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN=
如图,在正三棱柱ABC-A1 B1 C1中,AA1=4,AB=2,M是AC的中点,点N在AA1上,AN= 如图:在正三棱柱ABC-A1 B1 C1中,AB=
如图:在正三棱柱ABC-A1 B1 C1中,AB= =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a. =a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.
=a,E,F分别是BB1,CC1上的点且BE=a,CF=2a.