
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且a,b,c成等比数列,sinB= ![]() ,
,
(1)求 ![]() +
+ ![]() 的值;
的值;
(2)若 ![]()
![]() =12,求a+c的值.
=12,求a+c的值.
【答案】
(1)解:由a,b,c成等比数列,可得b2=ac,
由正弦定理可得,sin2B=sinAsinC,
则 ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]()
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() ;
;
(2)解: ![]()
![]() =12,即有cacosB=12,可得cosB>0,
=12,即有cacosB=12,可得cosB>0,
由sinB= ![]() ,可得cosB=
,可得cosB= ![]() =
= ![]() ,
,
即有ac=13,b2=13,
由余弦定理可得,cosB= ![]() =
= ![]() =
= ![]() ,
,
解得a+c=3 ![]() .
.
【解析】(1)运用等比数列的中项的性质,结合正弦定理,可得sin2B=sinAsinC,再由三角函数的恒等变换公式化简可得;(2)运用向量的数量积的定义和余弦定理,同角的平方关系,计算即可得到所求值.
【考点精析】通过灵活运用等比数列的通项公式(及其变式),掌握通项公式:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣ax+b(a>0,b>0)有两个不同的零点m,n,且m,n和﹣2三个数适当排序后,即可成为等差数列,也可成为等比数列,则a+b的值为( )
A.7
B.8
C.9
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如图所示的频率分布直方图.

(1)求这500件产品质量指标值的样本平均数![]() 和样本方差s2(同一组中的数据用该组区间的中点值作代表).
和样本方差s2(同一组中的数据用该组区间的中点值作代表).
(2)由直方图可以认为,这种产品的质量指标值Z服从正态分布N(μ,σ2),其中μ近似为样本平均数![]() ,σ2近似为样本方差s2.
,σ2近似为样本方差s2.
①利用该正态分布,求P(187.8<Z<212.2);
②某用户从该企业购买了100件这种产品,记X表示这100件产品中质量指标值位于区间(187.8,212.2)上的产品件数,利用①的结果,求E(X).
附:![]() ≈12.2.
≈12.2.
若Z~N(μ,σ2),则P(μ-σ<Z<μ+σ)=0.682 6,P(μ-2σ<Z<μ+2σ)=0.954 4.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 为参数),
为参数),![]() 为参数).
为参数).
(1)化![]() 的参数方程为普通方程,并说明它们分别表示什么曲线;
的参数方程为普通方程,并说明它们分别表示什么曲线;
(2)若![]() 上的点
上的点![]() 对应的参数为
对应的参数为![]() 为
为![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() 为参数)距离的最小值.
为参数)距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣2x,其中a≤0.
ax2﹣2x,其中a≤0.
(1)若曲线y=f(x)在点(1,f(1))处的切线方程为y=2x+b,求a﹣2b的值;
(2)讨论函数f(x)的单调性;
(3)设函数g(x)=x2﹣3x+3,如果对于任意的x,t∈(0,1],都有f(x)≤g(t)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在(﹣∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”.现有定义在(﹣∞,0)∪(0,+∞)上的如下函数:①f(x)=x2;②f(x)=2x;③f(x)= ![]() ;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
;④f(x)=ln|x|.则其中是“保等比数列函数”的f(x)的序号为( )
A.①②
B.③④
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(I)已知函数f(x)=rx﹣xr+(1﹣r)(x>0),其中r为有理数,且0<r<1.求f(x)的最小值;
(II)试用(I)的结果证明如下命题:设a1≥0,a2≥0,b1 , b2为正有理数,若b1+b2=1,则a1b1a2b2≤a1b1+a2b2;
(III)请将(II)中的命题推广到一般形式,并用数学归纳法证明你所推广的命题.注:当α为正有理数时,有求导公式(xα)r=αxα﹣1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: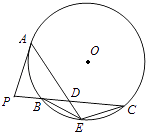
(1)BE=EC;
(2)ADDE=2PB2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com