
分析 由已知推导出a1+a2+a3=a4+a5+a6=a7+a8+a9=6,a10=3,由此能求出结果.
解答 解:∵数列{an}满足a1=3,an-1+an+an+1=6(n≥2),Sn=a1+a2+…+an,
∴a1+a2+a3=3+a2+a3=6,∴a2+a3=3,
又a2+a3+a4=6,∴a4=3,
又a4+a5+a6=3+a5+a6=6,∴a5+a6=3,
∴a5+a6+a7=3,∴a7=3,
∴a7+a8+a9=3+a8+a9=6,∴a8+a9=3,
∴a8+a9+a10=6,∴a10=3,
S10=(a1+a2+a3)+(a4+a5+a6)+(a7+a8+a9)+a10=6+6+6+3=21.
故答案为:21.
点评 本题考查数列的前10项和的求法,是中档题,解题时要认真审题,注意数列的递推公式的合理运用.


科目:高中数学 来源: 题型:填空题
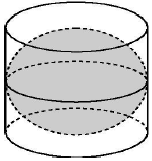 如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.
如图是古希腊数学家阿基米德的墓碑文,墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等.相传这个图形表达了阿基米德最引以自豪的发现.我们来重温这个伟大发现.经计算球的体积等于圆柱体积的$\frac{2}{3}$倍.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-1≤k≤\frac{5}{4}$ | B. | $-\frac{5}{4}≤k≤1$ | C. | $0≤k≤\frac{5}{4}$ | D. | $-\frac{5}{4}≤k≤0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1 | D. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com