【题目】已知在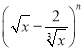
的展开式中，第5项的系数与第3项的系数之比是56：3．
（1）求展开式中的所有有理项；
（2）求展开式中系数绝对值最大的项．
（3）求
的值.
【答案】（1）T1=x5和T7=13400 ,（2）
,（3）
.
【解析】试题分析：（1）求二项展开式中特定项，关键在从通项出发，找寻对应等量关系. 由
解得n=10,因为通项：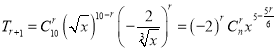 
,当5﹣
为整数，r可取0，6,于是有理项为T1=x5和T7=13400,（2）求展开式中系数绝对值最大的项，通过列不等式解决. 设第r+1项系数绝对值最大，则
,解得
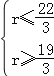，于是r只能为7,所以系数绝对值最大的项为,（3）本题是二项式定理的逆向应用,关键将式子转化符合二项展开式的特征. 
（1）由
解得n=10 （2分）
因为通项：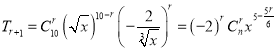 
（3分）
当5﹣为整数，r可取0，6 （4分）
展开式是常数项，于是有理项为T1=x5和T7=13400 （6分）
（2）设第r+1项系数绝对值最大，则
（8分）
注：等号不写扣（1分）
解得，于是r只能为7 （10分）
所以系数绝对值最大的项为（11分）
（3）
13分
.16分
53随堂测系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知椭圆
： 
的左，右焦点分别为
， 
.点
是椭圆
在
轴上方的动点，且△
的周长为16.
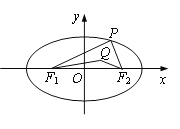
（1）求椭圆
的方程；
（2）设点
到△
三边的距离均相等.
①当
时，求点
的坐标；
②求证：点
在定椭圆上.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某医疗研究所开发一种新药，如果成人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y与时间t之间近似满足如图所示的曲线．
(1)写出服药后y与t之间的函数关系式；
(2)据测定，每毫升血液中含药量不少于4 μg时治疗疾病有效，假若某病人一天中第一次服药为上午7：00，问：一天中怎样安排服药时间(共4次)效果最佳？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆
与圆
的公共点的轨迹为曲线
，且曲线
与
轴的正半轴相交于点
．若曲线
上相异两点
满足直线
的斜率之积为
．
（1）求
的方程；
（2）证明直线
恒过定点，并求定点的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝(－x2＋x－1)ex，其中e是自然对数的底数．
(1)求曲线f(x)在点(1，f(1))处的切线；
(2)若方程f(x)＝
x3＋
x2＋m有3个不同的根，求实数m的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司从1999年的年产值100万元，增加到10年后2009年的500万元，如果每年产值增长率相同，则每年的平均增长率是多少？(ln(1＋x)≈x，lg2＝0.3，ln10＝2.30)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司生产电饭煲，每年需投入固定成本40万元，每生产1万件还需另投入16万元的变动成本，设该公司一年内共生产电饭煲
万件并全部销售完，每一万件的销售收入为
万元，且
（
），该公司在电饭煲的生产中所获年利润为
（万元），（注：利润=销售收入-成本）
（1）写出年利润
（万元）关于年产量
（万件）的函数解析式，并求年利润的最大值；
（2）为了让年利润
不低于2360万元，求年产量
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，一个树形图依据下列规律不断生长，1个空心圆点到下一行仅生长出1个实心圆点，1个实心圆点到下一行生长出1个实心圆点和1个空心圆点，则第11行的实心圆点的个数是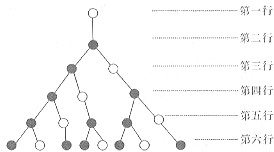
A. 21 B. 34 C. 55 D. 89
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com