
如图,已知正四棱锥R-ABCD的底面边长为4,高为6,点P是高的中点,点Q是侧面RBC的重心.求:

(1)异面直线PQ与BR所成的角;
(2)直线PQ与底面ABCD所成的角.
|
解:以正四棱锥的底面中心O为原点,过O平行于AD的直线为x轴建立空间直角坐标系,如图. 则R(0,0,6),B(2,2,0),C(-2,2,0), ∵P是RO的中点,Q是△RBC的重心, ∴P(0,0,3),Q(0, (1) ∴cos〈 ∴异面直线PQ与BR所成的角为arccos (2)方法一:∵RQ⊥底面ABCD, ∴RE在底面的射影为OE. ∵Q∈RE,∴Q在底面上的射影在OE上. ∴PQ在底面上的射影为OE. ∴∠REO为PQ与底面ABCD所成的角. ∵E(0,2,0),∴ ∴cos〈 ∴直线PQ与底面ABCD所成的角是arccos 方法二:平面ABCD的一个法向量为n=(0,0,1), ∴cos〈 ∵〈 |
|
本题考查了异面直线所成的角和直线与平面所成角的求法.通常有两种方法:(1)“找→求”的常规法;(2)向量法. |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
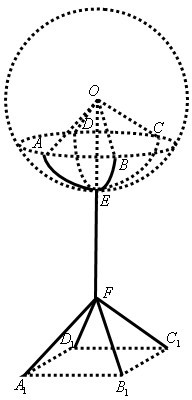 (2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托
(2013•江苏一模)某部门要设计一种如图所示的灯架,用来安装球心为O,半径为R(米)的球形灯泡.该灯架由灯托、灯杆、灯脚三个部件组成,其中圆弧形灯托 |
| EA |
 |
| EB |
 |
| EC |
 |
| ED |
| a |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2013年江苏省苏锡常镇、徐州、连云港六市高考数学一模试卷(解析版) 题型:解答题
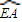 ,
,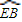 ,
,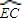 ,
,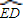 所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米
所在圆的圆心都是O、半径都是R(米)、圆弧的圆心角都是θ(弧度);灯杆EF垂直于地面,杆顶E到地面的距离为h(米),且h>R;灯脚FA1,FB1,FC1,FD1是正四棱锥F-A1B1C1D1的四条侧棱,正方形A1B1C1D1的外接圆半径为R(米),四条灯脚与灯杆所在直线的夹角都为θ(弧度).已知灯杆、灯脚的造价都是每米a(元),灯托造价是每米 (元),其中R,h,a都为常数.设该灯架的总造价为y(元).
(元),其中R,h,a都为常数.设该灯架的总造价为y(元).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com