练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在三棱锥中，，，平面平面，点在棱上.

    若为的中点，证明：.

    若与平面所成角的正弦值为，求.

    【答案】证明见解析；.

    【解析】

    取的中点，连接，.利用勾股定理求证，进而得，最后证出.

    以为坐标原点，的方向为轴正方向，的方向为轴正方向，的方向为轴正方向，建立空间直角坐标系，设，设平面的法向量为，根据与平面所成角的正弦值为，列式求得，进而求.

    解：证明：取的中点，连接，.因为，所以.

    又因为平面平面，且相交于，所以平面，

    所以.

    因为，所以，

    所以，所以，

    所以，且为的中点，所以.

    解：如图，以为坐标原点，的方向为轴正方向，的方向为轴正方向，的方向为轴正方向，建立空间直角坐标系，由已知得，，，，，

    设，

    则.

    设平面的法向量为.

    由，，得，

    可取，

    所以，

    解得（舍去），，则

    所以.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，AB是平面的斜线段，A为斜足，点C满足，且在平面内运动，则有以下几个命题：

    ①当时，点C的轨迹是抛物线；

    ②当时，点C的轨迹是一条直线；

    ③当时，点C的轨迹是圆；

    ④当时，点C的轨迹是椭圆；

    ⑤当时，点C的轨迹是双曲线.

    其中正确的命题是__________.（将所有正确的命题序号填到横线上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数，，其中为欧拉数，，为未知实数，且.如果和均为函数的单调区间.

    （1）求；

    （2）若函数在上有极值点，为实数，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大型商场的空调在1月到5月的销售量与月份相关，得到的统计数据如下表：

    月份

    1

    2

    3

    4

    5

    销量（百台）

    0.6

    0.8

    1.2

    1.6

    1.8

    （1）经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量（百件）与月份之间的相关关系.请用最小二乘法求关于的线性回归方程，并预测6月份该商场空调的销售量；

    （2）若该商场的营销部对空调进行新一轮促销，对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大，经过营销部调研机构对其中的500名顾客进行了一个抽样调查，得到如下一份频数表：

    有购买意愿对应的月份

    7

    8

    9

    10

    11

    12

    频数

    60

    80

    120

    130

    80

    30

    现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名，再从这6人中随机抽取3人进行跟踪调查，求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.

    参考公式与数据：线性回归方程，其中，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    讨论极值点的个数；

    若有两个极值点，证明：的极大值大于.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，，，，，，.过直线的平面分别交棱，于E，F两点.

    （1）求证：；

    （2）若直线与平面所成角为，且，，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】植物园拟建一个多边形苗圃，苗圃的一边紧靠着长度大于30m的围墙．现有两种方案：

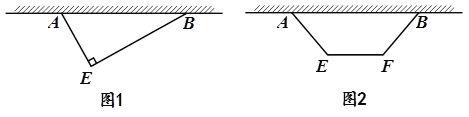
    方案① 多边形为直角三角形（），如图1所示，其中；

    方案② 多边形为等腰梯形（），如图2所示，其中．

    请你分别求出两种方案中苗圃的最大面积，并从中确定使苗圃面积最大的方案．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，分别是双曲线的左，右焦点，过点向一条渐近线作垂线，交双曲线右支于点，直线与轴交于点（，在轴同侧），连接，若的内切圆圆心恰好落在以为直径的圆上，则的大小为________；双曲线的离心率为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司为提高市场销售业绩，促进某产品的销售，随机调查了该产品的月销售单价（单位：元/件）及相应月销量（单位：万件），对近5个月的月销售单价和月销售量的数据进行了统计，得到如下表数据：

    月销售单价（元/件）

    9

    10

    11

    月销售量（万件）

    11

    10

    8

    6

    5

    （Ⅰ）建立关于的回归直线方程；

    （Ⅱ）该公司开展促销活动，当该产品月销售单价为7元/件时，其月销售量达到18万件，若由回归直线方程得到的预测数据与此次促销活动的实际数据之差的绝对值不超过万件，则认为所得到的回归直线方程是理想的，试问：（Ⅰ）中得到的回归直线方程是否理想？

    （Ⅲ）根据（Ⅰ）的结果，若该产品成本是5元/件，月销售单价为何值时（销售单价不超过11元/件），公司月利润的预计值最大？

    参考公式：回归直线方程，其中，．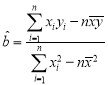

    参考数据：，．

    查看答案和解析>>

    同步练习册答案