
【题目】在![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 所对的边分别为
所对的边分别为![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() 的面积
的面积![]() ,求
,求![]() 和
和![]() 的值.
的值.
【答案】(1)![]() .(2)
.(2)![]() ,
,![]() .
.
【解析】试题分析 :(Ⅰ)由余弦定理可以解出cosC;
(Ⅱ)用二倍角的余弦公式对方程进行化简,结合所给的面积解出a=3,b=3,
试题解析:(1)由题意知,![]() ,
,
由余弦定理,得![]()
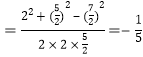 .
.
(2)∵![]() ,由正弦定理可知,
,由正弦定理可知,![]() ,
,
又因![]() ,故
,故![]() ,
,
由于![]() ,
,
∴![]() ,从而
,从而![]() ,
,
解得![]() ,
,![]() .
.
点晴:在处理解三角形问题时,要注意抓住题目所给的条件,当题设中给定三角形的面积,可以使用面积公式建立等式,再将所有边的关系转化为角的关系,有时需将角的关系转化为边的关系;解三角形问题常见的一种考题是“已知一条边的长度和它所对的角,求面积或周长的取值范围”或者“已知一条边的长度和它所对的角,再有另外一个条件,求面积或周长的值”。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和. (Ⅰ)若2Sn=3n+3.求{an}的通项公式;
(Ⅱ)若a1=1,an+1﹣an=2n(n∈N*),求Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
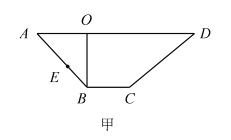
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
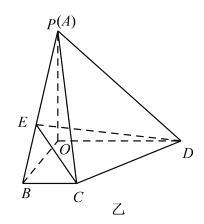
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知各项均为正数的等比数列{an}中,a2=4,a4=16.
(1)求公比q;
(2)若a3 , a5分别为等差数列{bn}的第3项和第5项,求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从装有![]() 个红球和
个红球和![]() 个黑球的口袋内任取
个黑球的口袋内任取![]() 个球,那么互斥而不对立的两个事件是( )
个球,那么互斥而不对立的两个事件是( )
A. 至少有一个黑球与都是黑球 B. 至少有一个黑球与都是红球
C. 至少有一个黑球与至少有![]() 个红球 D. 恰有
个红球 D. 恰有![]() 个黑球与恰有
个黑球与恰有![]() 个黑球
个黑球
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米. 
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M=( ![]() ﹣1)(
﹣1)( ![]() ﹣1)(
﹣1)( ![]() ﹣1)满足a+b+c=1(其中a>0,b>0,c>0),则M的取值范围是( )
﹣1)满足a+b+c=1(其中a>0,b>0,c>0),则M的取值范围是( )
A.[0, ![]() )
)
B.[ ![]() ,1)
,1)
C.[1,8)
D.[8,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com