
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形
![]() 为矩形,平面
为矩形,平面![]() 平面
平面![]() ,
,![]() .
.
(I)求证:![]() 平面
平面![]() ;
;
(II)点![]() 在线段
在线段![]() 上运动,设平面
上运动,设平面![]() 与平面
与平面![]() 所成二面角的平面角为
所成二面角的平面角为![]() ,
,
试求![]() 的取值范围.
的取值范围.

【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)由题意结合勾股定理和余弦定理可证得BC⊥AC,结合面面垂直的性质定理可得BC⊥平面ACFE.
(2)以CA,CB,CF所在的直线为x轴,y轴,z轴建立空间直角坐标系,由题意可得平面MAB的一个法向量n1=(1,![]() ,
,![]() -λ),平面FCB的一个法向量n2=(1,0,0),则 cosθ=
-λ),平面FCB的一个法向量n2=(1,0,0),则 cosθ=![]() ,结合三角函数的性质可得cosθ∈[
,结合三角函数的性质可得cosθ∈[![]() ,
,![]() ].
].
(1)在梯形ABCD中,∵AB∥CD,AD=DC=CB=1,∠ABC=60°,
∴AB=2,∴AC2=AB2+BC2-2AB·BC·cos 60°=3,
∴AB2=AC2+BC2,∴BC⊥AC.
又平面ACFE⊥平面ABCD,平面ACFE∩平面ABCD=AC,BC平面ABCD,
∴BC⊥平面ACFE.
(2)由(1)知,可分别以CA,CB,CF所在的直线为x轴,y轴,z轴建立如图所示的空间直角坐标系,
令FM=λ(0≤λ≤![]() ),则C(0,0,0),A(
),则C(0,0,0),A(![]() ,0,0),B(0,1,0),M(λ,0,1),
,0,0),B(0,1,0),M(λ,0,1),
∴![]() =(-
=(-![]() ,1,0),
,1,0),![]() =(λ,-1,1).
=(λ,-1,1).
设n1=(x,y,z)为平面MAB的法向量,
由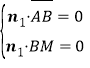 ,得
,得![]() ,
,
取x=1,则n1=(1,![]() ,
,![]() -λ)为平面MAB的一个法向量,
-λ)为平面MAB的一个法向量,
易知n2=(1,0,0)是平面FCB的一个法向量,
∴ cosθ=![]() .
.
∵0≤λ≤![]() , ∴当λ=0时,cosθ有最小值
, ∴当λ=0时,cosθ有最小值![]() , 当λ=
, 当λ=![]() 时,cosθ有最大值
时,cosθ有最大值![]() ,∴cosθ∈[
,∴cosθ∈[![]() ,
,![]() ].
].


科目:高中数学 来源: 题型:
【题目】在如图所示的三棱锥ABC﹣A1B1C1中,AA1⊥底面ABC,D,E分别是BC,A1B1的中点. 
(1)求证:DE∥平面ACC1A1;
(2)若AB⊥BC,AB=BC,∠ACB1=60°,求直线BC与平面AB1C所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,已知圆C的圆心坐标为(2,0),半径为 ![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为:
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.,直线l的参数方程为: ![]() (t为参数).
(t为参数).
(1)求圆C和直线l的极坐标方程;
(2)点P的极坐标为(1, ![]() ),直线l与圆C相交于A,B,求|PA|+|PB|的值.
),直线l与圆C相交于A,B,求|PA|+|PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个线性回归方程![]() ,变量x增加1个单位时,y平均增加5个单位;
,变量x增加1个单位时,y平均增加5个单位;
③设具有相关关系的两个变量x,y的相关系数为r,则|r|越接近于0,x和y之间的线性相关程度越强;
④在一个2×2列联表中,由计算得K2的值,则K2的值越大,判断两个变量间有关联的把握就越大.
以上错误结论的个数为( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.
(1)求S=![]() 的概率;
的概率;
(2)求S的分布列及数学期望E(S).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com