
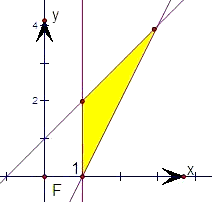
 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| x+y |
| 1+xy |
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 用特征性质描述法表示图中阴影部分的点(含边界上的点)组成的集合M是
用特征性质描述法表示图中阴影部分的点(含边界上的点)组成的集合M是
|
|
|
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:解答题
 ;
; ,判断是否有h(x)∈M,说明理由;
,判断是否有h(x)∈M,说明理由; ,求函数
,求函数 的所有零点.
的所有零点.查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省成都七中高一(上)期中数学试卷(解析版) 题型:解答题
 ;
; ,判断是否有h(x)∈M,说明理由;
,判断是否有h(x)∈M,说明理由; ,求函数
,求函数 的所有零点.
的所有零点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com