
【题目】函数 f(x)=2x﹣ ![]() 的定义域为(0,1](a为实数).
的定义域为(0,1](a为实数).
(Ⅰ)当a=﹣1时,求函数y=f(x)的值域;
(Ⅱ)若函数y=f(x)在定义域上是减函数,求a的取值范围;
(Ⅲ)求函数y=f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值.
【答案】解:(Ⅰ)显然函数y=f(x)的值域为 ![]() ;
;
(Ⅱ)若函数y=f(x)在定义域上是减函数,则:f'(x)=2+![]()
![]() 0
0![]() a
a![]() a--2x2
a--2x2![]() 在定义域上恒成立
在定义域上恒成立
而﹣2x2∈[﹣2,0)
∴a≤﹣2
(II)当a≥0时,函数y=f(x)在(0.1]上单调递增,无最小值,
当x=1时取得最大值2﹣a;
由(2)得当a≤﹣2时,函数y=f(x)在(0.1]上单调递减,无最大值,
当x=1时取得最小值2﹣a;
当﹣2<a<0时,函数y=f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,无最大值,
上单调递增,无最大值,
当 ![]() 时取得最小值
时取得最小值 ![]()
【解析】(1)a=﹣1时,函数为对勾函数,结合函数图像可直接写出函数的值域.
(2)函数y=f(x)在定义域上是减函数,则 f '( x ) ![]() 0,再进行分离变量进行求解.
0,再进行分离变量进行求解.
(3)对a进行分情况讨论,结合函数的单调性求解函数的最值.
【考点精析】根据题目的已知条件,利用函数的值域和函数的最大(小)值与导数的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】已知函数 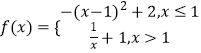 下列四个命题:
下列四个命题:
①f(f(1))>f(3); ② ![]() x0∈(1,+∞),f'(x0)=-1/3;
x0∈(1,+∞),f'(x0)=-1/3;
③f(x)的极大值点为x=1; ④ ![]() x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
x1,x2∈(0,+∞),|f(x1)-f(x2)|≤1
其中正确的有(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数y=f(x)定义域是R,当x≥0时,f(x)=x(1﹣x).
(1)求出函数y=f(x)的解析式;
(2)写出函数y=f(x)的单调递增区间.(不用证明,只需直接写出递增区间即可)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,M、N分别是棱AB、CC1的中点,△MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
①平面MB1P⊥ND1;②平面MB1P⊥平面ND1A1;③△MB1P在底面ABCD上的射影图形的面积为定值;④△MB1P在侧面D1C1CD上的射影图形是三角形.
其中正确命题的序号是 . 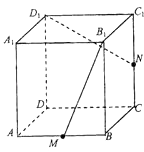
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+
+2x+sinx(x∈R),若函数y=f(x2+2)+f(﹣2x﹣m)只有一个零点,则函数g(x)=mx+ ![]() (x>1)的最小值是 .
(x>1)的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线 ![]() 是函数f(x)=sinx+acosx的图象的一条对称轴.
是函数f(x)=sinx+acosx的图象的一条对称轴.
(1)求函数f(x)的最大值及取得最大值时x的值;
(2)求函数f(x)在[0,π]上的减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C是圆O上的三个点,CO的延长线与线段BA的延长线交于圆外一点.若 ![]() ,其中m,n∈R.则m+n的取值范围是( )
,其中m,n∈R.则m+n的取值范围是( )
A.(0,1)
B.(﹣1,0)
C.(1,+∞)
D.(﹣∞,﹣1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com