
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 参数方程为:
参数方程为:![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 交点分别为
交点分别为![]() ,
,![]() ,求
,求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() ,斜率为
,斜率为![]() 的直线交抛物线于
的直线交抛物线于![]() 两点,且
两点,且![]() .
.
(1)求该抛物线![]() 的方程;
的方程;
(2)过点![]() 任意作互相垂直的两条直线
任意作互相垂直的两条直线![]() ,分别交曲线
,分别交曲线![]() 于点
于点![]() 和
和![]() .设线段
.设线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 恒过一个定点.
恒过一个定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数u(x)=xlnx,v(x)![]() x﹣1,m∈R.
x﹣1,m∈R.
(1)令m=2,求函数h(x)![]() 的单调区间;
的单调区间;
(2)令f(x)=u(x)﹣v(x),若函数f(x)恰有两个极值点x1,x2,且满足1![]() e(e为自然对数的底数)求x1x2的最大值.
e(e为自然对数的底数)求x1x2的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】哈师大附中高三学年统计甲、乙两个班级一模数学分数(满分150分),每个班级20名同学,现有甲、乙两位同学的20次成绩如下列茎叶图所示:
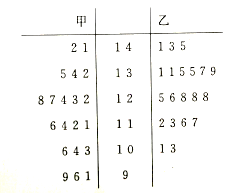
(I)根据基叶图求甲、乙两位同学成绩的中位数,并将乙同学的成绩的频率分布直方图填充完整;
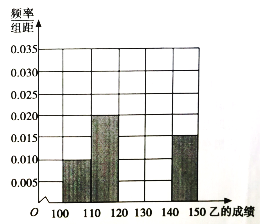
(Ⅱ)根据基叶图比较甲乙两位同学数学成绩的平均值及稳定程度(不要求计算出具体值,给出结论即可)
(Ⅲ)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设事件![]() 为“其中2 个成绩分别属于不同的同学”,求事件
为“其中2 个成绩分别属于不同的同学”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() :
:![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() .
.
(1)求![]() 的方程;
的方程;
(2)斜率为![]() (
(![]() )的直线
)的直线![]() 过线段
过线段![]() 的中点,与
的中点,与![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别交直线
分别交直线![]() 于
于![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家放开计划生育政策,鼓励一对夫妇生育2个孩子.在某地区的100000对已经生育了一胎夫妇中,进行大数据统计得,有100对第一胎生育的是双胞胎或多胞胎,其余的均为单胞胎.在这99900对恰好生育一孩的夫妇中,男方、女方都愿意生育二孩的有50000对,男方愿意生育二孩女方不愿意生育二孩的有![]() 对,男方不愿意生育二孩女方愿意生育二孩的有
对,男方不愿意生育二孩女方愿意生育二孩的有![]() 对,其余情形有
对,其余情形有![]() 对,且
对,且![]() .现用样本的频率来估计总体的概率.
.现用样本的频率来估计总体的概率.
(1)说明“其余情形”指何种具体情形,并求出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)该地区为进一步鼓励生育二孩,实行贴补政策:凡第一胎生育了一孩的夫妇一次性贴补5000元,第一胎生育了双胞胎或多胞胎的夫妇只有一次性贴补15000元.第一胎已经生育了一孩再生育了二孩的夫妇一次性再贴补20000元.这种补贴政策直接提高了夫妇生育二孩的积极性:原先男方或女方中只有一方愿意生育二孩的夫妇现在都愿意生育二孩,但原先男方、女方都不愿意生育二孩的夫妇仍然不愿意生育二孩.设![]() 为该地区的一对夫妇享受的生育贴补,求
为该地区的一对夫妇享受的生育贴补,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com