


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
设![]() 是空间两个不同的平面,m,n是平面
是空间两个不同的平面,m,n是平面![]() 及
及![]() 外的两条不同直线.从“①m⊥n;②
外的两条不同直线.从“①m⊥n;②![]() ⊥
⊥![]() ;③n⊥
;③n⊥![]() ;④m⊥
;④m⊥![]() ”中选取三个作为条件,余下一个作为结论组成命题,其中为真命题的个数是 A.4 B.3 C.2 D. 1
”中选取三个作为条件,余下一个作为结论组成命题,其中为真命题的个数是 A.4 B.3 C.2 D. 1
查看答案和解析>>
科目:高中数学 来源:2011届江苏省南通市高三第一次调研测试数学文卷 题型:填空题
设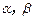 是空间两个不同的平面,m,n是平面
是空间两个不同的平面,m,n是平面 及
及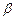 外的两条不同直线.从“①m⊥n;②
外的两条不同直线.从“①m⊥n;② ⊥
⊥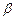 ;③n⊥
;③n⊥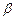 ;④m⊥
;④m⊥ ”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: ▲ (用代号表示).
”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: ▲ (用代号表示).
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市高三第二次模拟考试数学试题 题型:填空题
设 是空间两个不同的平面,m,n是平面
是空间两个不同的平面,m,n是平面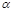 及
及 外的两条不同直线.从“①m⊥n;②
外的两条不同直线.从“①m⊥n;② ⊥
⊥ ;③n⊥
;③n⊥ ;④m⊥
;④m⊥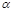 ”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: ▲ (用代号表示)
”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题: ▲ (用代号表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com