
【题目】已知f(x)=axex﹣lnx﹣x.
(Ⅰ)若f(x)有两个不同的零点,求实数a的取值范围;
(Ⅱ)已知a=1,若对任意的x>0,均有f(x)>cx2﹣2x+1成立,求实数c的取值范围.
【答案】(Ⅰ)0<a![]() .(Ⅱ)c≤e.
.(Ⅱ)c≤e.
【解析】
(Ⅰ)先求导![]() ,得
,得![]() ,分两种情况
,分两种情况![]() ,讨论函数
,讨论函数![]() 单调性,求出
单调性,求出![]() 最值,再结合函数
最值,再结合函数![]() 有两个不同的零点求出
有两个不同的零点求出![]() 的取值范围.
的取值范围.
(Ⅱ)因为![]() f(x)≥cx2-2x+1对
f(x)≥cx2-2x+1对![]() 恒成立,则
恒成立,则![]() ,得
,得![]() .再证明,当
.再证明,当![]() 时,f
时,f![]() ,对
,对![]() 恒成立,即可.
恒成立,即可.
(Ⅰ)![]() ,
,
若a≤0,则f′(x)<0,f(x)在(0,+∞)上单调递减,不合题意.
若a>0,y=axex在(0,+∞)上递增,必存在唯一的x0∈(0,+∞),使得ax0e![]() 1,
1,
此时,x∈(0,x0)时,f′(x)<0,f(x)递减,且当x→0+ 时,f(x)→+∞,
当x∈(x0,+∞)时,f′(x)>0,f(x)递增,且当x→+∞时,f(x)→+∞,
故f(x)min=f(x0)=ax0e![]() lnx0﹣x0,
lnx0﹣x0,
因为ax0e![]() 1,可得lna+lnx0+x0=0,
1,可得lna+lnx0+x0=0,
所以f(x)max=1+lna,
由题意得,1+lna<0,得a∈(0,![]() ),
),
综上,可得所求的取值范围是0<a![]() .
.
(Ⅱ)因为f(x)≥cx2﹣2x+1对x>0恒成立,
则f(1)≥c﹣2+1,得c≤e.
下证,当c≤e时,f(x)≥cx2﹣2x+1,对x>0恒成立
事实上f(x)≥cx2﹣2x+1xex﹣lnx+x﹣1﹣cx2≥0,
注意到lnx≤x﹣1,故只需证xex﹣cx2≥0,
只需证ex≥cx,因为ex≥ex≥cx,结论得证,
综上可知c的取值范围是c≤e.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(1)求{an}和{bn}的通项公式;
(2)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某中学学生会对本校高一年级1000名学生课余时间参加传统文化活动的情况,随机抽取50名学生进行调查,将数据分组整理后,列表如下:
参加场数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
参加人数占调查人数的百分比 | 8% | 10% | 20% | 26% | 18% | 12% | 4% | 2% |
估计该校高一学生参加传统文化活动情况正确的是().
A. 参加活动次数是3场的学生约为360人B. 参加活动次数是2场或4场的学生约为480人
C. 参加活动次数不高于2场的学生约为280人D. 参加活动次数不低于4场的学生约为360人
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(a>b>0)的一个焦点是(1,0),两个焦点与短轴的一个端点构成等边三角形.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是直角梯形,AB∥CD,BC⊥CD,侧面PAB为等边三角形,AB=BC=2CD=2.
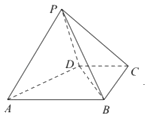
(Ⅰ)证明:AB⊥PD;
(Ⅱ)若PD=2,求直线PC与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
已知椭圆![]() :
:![]() 的左、右顶点分别为A,B,其离心率
的左、右顶点分别为A,B,其离心率![]() ,点
,点![]() 为椭圆上的一个动点,
为椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)若过椭圆![]() 右顶点
右顶点![]() 的直线
的直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() ,线段
,线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区随着经济的发展,居民收入逐年增长,银行储蓄连年增长,下表是该地区某银行连续五年的储蓄存款(年底结算):
年份 |
|
|
|
|
|
储蓄存款 |
|
|
|
|
|
为方便研究,工作人员对上表的数据做了如下处理:![]() ,
,![]() 得到下表:
得到下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)通过(1)中的方程,求出![]() 关于
关于![]() 的线性回归方程,并用所求回归方程预测
的线性回归方程,并用所求回归方程预测![]() 年底,该地储蓄存款额可达多少?
年底,该地储蓄存款额可达多少?
(附:参考公式![]() ,其中
,其中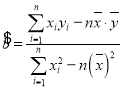 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点E是圆心为O1半径为2的半圆弧上从点B数起的第一个三等分点,点F是圆心为O2半径为1的半圆弧的中点,AB、CD分别是两个半圆的直径,O1O2=2,直线O1O2与两个半圆所在的平面均垂直,直线AB、DC共面.
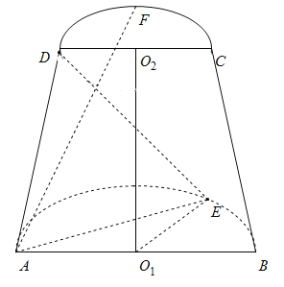
(1)求三棱锥D﹣ABE的体积;
(2)求直线DE与平面ABE所成的角的正切值;
(3)求直线AF与BE所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com