
【题目】已知函数f(x)=|x+4|﹣|x﹣1|.
(1)解不等式f(x)>3;
(2)若不等式f(x)+1≤4a﹣5×2a有解,求实数a的取值范围.
【答案】
(1)解:由题意可得 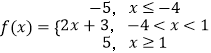 ,
,
则当x≤﹣4时,不成立;当﹣4<x<1时,2x+3>3,解得0<x<1;
当x≥1时,5>3成立,故原不等式的解集为{x|x>0}
(2)解:根据题意可得 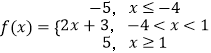 的最小值为﹣5,
的最小值为﹣5,
由即f(x)≤4a﹣5×2a﹣1有解,∴4a﹣5×2a﹣1≥﹣5,即4a﹣5×2a+4≥0,即2a≥4或2a≤1,∴a≥2或a≤0,
故实数a的取值范围是(﹣∞,0]∪[2,+∞)
【解析】(1)由题意可得 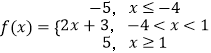 ,分类讨论,求得不等式f(x)>3的解集.(2)根据题意可得
,分类讨论,求得不等式f(x)>3的解集.(2)根据题意可得 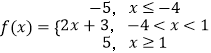 的最小值为﹣5,可得4a﹣5×2a﹣1≥﹣5,由此求得实数a的取值范围.
的最小值为﹣5,可得4a﹣5×2a﹣1≥﹣5,由此求得实数a的取值范围.
【考点精析】认真审题,首先需要了解绝对值不等式的解法(含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinωx,其中常数ω>0.
(Ⅰ)令ω=1,求函数 ![]() 在
在 ![]() 上的最大值;
上的最大值;
(Ⅱ)若函数 ![]() 的周期为π,求函数g(x)的单调递增区间,并直接写出g(x)在
的周期为π,求函数g(x)的单调递增区间,并直接写出g(x)在 ![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=x2﹣bx+c满足f(1+x)=f(1﹣x)且f(0)=3,则f(bx)和f(cx)的大小关系是( )
A.f(bx)≤f(cx)
B.f(bx)≥f(cx)
C.f(bx)>f(cx)
D.大小关系随x的不同而不同
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,PD⊥面ABCD,底面ABCD是菱形,且PD=DA=2,∠CDA=60°,过点B作直线l∥PD,Q为直线l上一动点. 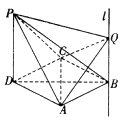
(1)求证:QP⊥AC;
(2)当二面角Q﹣AC﹣P的大小为120°时,求QB的长;
(3)在(2)的条件下,求三棱锥Q﹣ACP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x2﹣a)e1﹣x , g(x)=f(x)+ae1﹣x﹣a(x﹣1).
(1)讨论f(x)的单调性;
(2)当a=1时,求g(x)在( ![]() ,2)上的最大值;
,2)上的最大值;
(3)当f(x)有两个极值点x1 , x2(x1<x2)时,总有x2f(x1)≤λg′(x1),求实数λ的值(g′(x)为g(x)的导函数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com