
【题目】2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后得到年龄如图所示的频率分布直方图.
后得到年龄如图所示的频率分布直方图.

(1)试求这40人年龄的众数、中位数的估计值;
(2)(i)若从样本中年龄在![]() 的居民中任取2人赠送健身卡,求这2人中至少有1人年龄低于60岁的概率;
的居民中任取2人赠送健身卡,求这2人中至少有1人年龄低于60岁的概率;
(ii)己知该小区年龄在![]() 内的总人数为1200,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
内的总人数为1200,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.
【答案】(1)众数35,中位数35;(2)(i)![]() ,(ii)1056
,(ii)1056
【解析】
(1)根据频率分布直方图求众数和中位数的方法计算求解;
(2)(i)根据频率分布直方图求出年龄在![]() 的有4人,年龄在
的有4人,年龄在![]() 的有2人,利用列举法根据古典概型求解概率;(ii)根据频率分布直方图计算出年龄不超过80岁的成年人的频率即可得解.
的有2人,利用列举法根据古典概型求解概率;(ii)根据频率分布直方图计算出年龄不超过80岁的成年人的频率即可得解.
(1)由频率分布直方图可得众数的估计值为35,
前三组频率之分别为0.15,0.2,0.3,所以中位数在第三组,设为x,
则![]() ,解得
,解得![]()
所以中位数的估计值为35;
(2)(i)若从样本中年龄在![]() 的人数共
的人数共![]() 人,
人,
其中年龄在![]() 的有4人,设为
的有4人,设为![]() ,年龄在
,年龄在![]() 的有2人,设为
的有2人,设为![]() ,
,
从中任选2人,所有基本事件为:
![]() ,共15种,
,共15种,
至少有1人年龄低于60岁包含的基本事件为:
![]() ,共14种,
,共14种,
所以这2人中至少有1人年龄低于60岁的概率![]() ;
;
(ii)样本中年龄不超过80岁的成年人的频率为![]() ,
,
可以估计该小区年龄不超过80岁的成年人人数![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() 分别是
分别是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 折起,下列说法正确的是__________(填上所有正确的序号).
折起,下列说法正确的是__________(填上所有正确的序号).
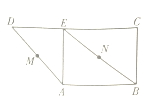
①不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内)都有
内)都有![]() 平面
平面![]() ;
;
②不论![]() 折至何位置都有
折至何位置都有![]() ;
;
③不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内)都有
内)都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了促进学生的全面发展,某市教育局要求本市所有学校重视社团文化建设,2014年该市某中学的某新生想通过考核选拨进入该校的“电影社”和“心理社”,已知该同学通过考核选拨进入这两个社团成功与否相互独立根据报名情况和他本人的才艺能力,两个社团都能进入的概率为![]() ,至少进入一个社团的概率为
,至少进入一个社团的概率为![]() ,并且进入“电影社”的概率小于进入“心理社”的概率
,并且进入“电影社”的概率小于进入“心理社”的概率
(Ⅰ)求该同学分别通过选拨进入“电影社”的概率![]() 和进入心理社的概率
和进入心理社的概率![]() ;
;
(Ⅱ)学校根据这两个社团的活动安排情况,对进入“电影社”的同学增加1个校本选修课学分,对进入“心理社”的同学增加0.5个校本选修课学分.求该同学在社团方面获得校本选修课学分分数不低于1分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图像向左平移
的图像向左平移![]() 个单位后得到函数
个单位后得到函数![]() 的图像,且函数
的图像,且函数![]() 满足
满足![]() ,则下列命题中正确的是()
,则下列命题中正确的是()
A. 函数![]() 图像的两条相邻对称轴之间的距离为
图像的两条相邻对称轴之间的距离为![]()
B. 函数![]() 图像关于点
图像关于点![]() 对称
对称
C. 函数![]() 图像关于直线
图像关于直线![]() 对称
对称
D. 函数![]() 在区间
在区间![]() 内为单调递减函数
内为单调递减函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com