
【题目】在 △ABC 中,设 a,b,c 分别是角 A,B,C 的对边,已知向量 ![]() = (a,sinC-sinB),
= (a,sinC-sinB),![]() = (b + c,sinA + sinB),且
= (b + c,sinA + sinB),且![]()
(1) 求角 C 的大小
(2) 若 c = 3, 求 △ABC 的周长的取值范围.
科目:高中数学 来源: 题型:
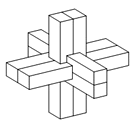
【题目】如图为中国传统智力玩具鲁班锁,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即樟卯结构)啮合,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称,六根完全相同的正四棱柱分成三组,经90°榫卯起来.现有一鲁班锁的正四校柱的底面正方形边长为1,欲将其放入球形容器内(容器壁的厚度忽略不计),若球形容器表面积的最小值为30π,则正四棱柱的高为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C对应边分别为a、b、c.
(1)若a=14,b=40,cosB=![]() ,求cosC;
,求cosC;
(2)若a=3,b=![]() ,B=2A,求c的长度.
,B=2A,求c的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() -
-![]() =1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于
=1(a>0,b>0)的离心率为2,焦点到渐近线的距离等于![]() ,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
,过右焦点F2的直线l交双曲线于A,B两点,F1为左焦点.
(1)求双曲线的方程;
(2)若△F1AB的面积等于6![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.

(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一个社区微信群“步行者”有成员100人,其中男性70人,女性30人,现统计他们平均每天步行的时间,得到频率分布直方图,如图所示:

若规定平均每天步行时间不少于2小时的成员为“步行健将”,低于2小时的成员为“非步行健将”.已知“步行健将”中女性占![]() .
.
(1)填写下面![]() 列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;
列联表,并通过计算判断能否在犯错误的概率不超过0.05的前提下认为“是否为‘步行健将’与性别有关”;

(2)现从“步行健将”中随机选派2人参加全市业余步行比赛,求2人中男性的人数![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABC—DEF中,若AB//DE,BC//EF.
(1)求证:平面ABC//平面DEF;
(2)已知![]() 是二面角C-AD-E的平面角.求证:平面ABC
是二面角C-AD-E的平面角.求证:平面ABC![]() 平面DABE.
平面DABE.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com