
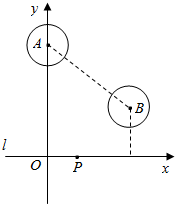
 如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).
如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).分析 (1)求出圆的圆心坐标,即可写出圆的方程.
(2)圆A关于x轴对称的圆为圆D,求出D(0,-55)又B(40,25),求出直线BD的方程为2x-y-55=0,当D,P,B三点共线时DP+BP最小即AP+BP最小,求出P的坐标.
解答 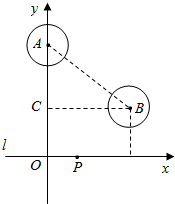 解:作BC⊥OA于点C,则在直角△ABC中,AB=50,AC=55-25=30,
解:作BC⊥OA于点C,则在直角△ABC中,AB=50,AC=55-25=30,
所以BC=40,
又B到x轴的距离为25,
所以B(40,25)…(3分)
所以圆B的方程为(x-40)2+(y-25)2=100.…(6分)
(2)设圆A关于x轴对称的圆为圆D,
则圆D:x2+(y+55)2=100,…(8分)
D(0,-55)又B(40,25)
所以${k_{DB}}=\frac{25-(-55)}{40-0}=2$
所以直线BD的方程为2x-y-55=0…(10分)
因为AP=DP,
所以AP+BP=DP+BP,
所以当点D,P,B三点共线时DP+BP最小即AP+BP最小,
最小值为$\sqrt{{{40}^2}+{{80}^2}}=40\sqrt{5}$…(14分).
由$\left\{\begin{array}{l}x-2y-55=0\\ y=0\end{array}\right.$,
解得P(0,$\frac{55}{2}$).…(16分)
点评 本题考查圆的方程的综合应用,直线与圆的位置关系,考查计算能力.


科目:高中数学 来源: 题型:选择题
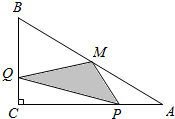 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,2] | B. | [-1,4] | C. | [$\frac{1}{2}$,4] | D. | [$\frac{1}{2}$,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com