
【题目】已知圆![]() 及直线
及直线![]() ,直线
,直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(![]() )求实数
)求实数![]() 的值.
的值.
(![]() )求过点
)求过点![]() 并与圆
并与圆![]() 相切的切线方程.
相切的切线方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
试题分析:(1)根据圆的方程找出圆心坐标与圆的半径,然后利用点到直线的距离公式表示出圆心到直线![]() 的距离
的距离![]() ,然后根据垂径定理得到弦心距,弦的一半及圆的半径成直角三角形,利用勾股对了列出关于
,然后根据垂径定理得到弦心距,弦的一半及圆的半径成直角三角形,利用勾股对了列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,然后由
的值,然后由![]() 大于0,得到满足题意
大于0,得到满足题意![]() 的值;(2)把(1)求出
的值;(2)把(1)求出![]() 的值代入圆的方程中确定出圆的方程,即可得到圆心的坐标,并判断得到已知点在圆外,分两种情况:当切线的斜率不存在时,得到
的值代入圆的方程中确定出圆的方程,即可得到圆心的坐标,并判断得到已知点在圆外,分两种情况:当切线的斜率不存在时,得到![]() 为圆的切线;当切线的斜率存在时,设切线的斜率为
为圆的切线;当切线的斜率存在时,设切线的斜率为![]() ,由
,由![]() 和设出的
和设出的![]() 写出切线的方程,根据直线与圆相切时圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到切线的距离
写出切线的方程,根据直线与圆相切时圆心到直线的距离等于圆的半径,利用点到直线的距离公式表示出圆心到切线的距离![]() ,让
,让![]() 等于圆的半径即可列出关于
等于圆的半径即可列出关于![]() 的方程,求出方程的解即可得到
的方程,求出方程的解即可得到![]() 的值,把
的值,把![]() 的值代入所设的切线方程即可确定出切线的方程.
的值代入所设的切线方程即可确定出切线的方程.
试题解析:(![]() )根据题意可得圆心
)根据题意可得圆心![]() ,半径
,半径![]() ,则圆心到直线
,则圆心到直线![]() 的距离
的距离![]() ,
,
由勾股定理可以知道![]() ,代入化简得
,代入化简得![]() ,
,
解得![]() 或
或![]() ,
,
又![]() ,
,
所以![]() .
.
(![]() )由(
)由(![]() )知圆
)知圆![]() ,圆心为
,圆心为![]() ,半径
,半径![]() ,
,
点![]() 到圆心的距离为
到圆心的距离为![]() ,故点
,故点![]() 在圆外,
在圆外,
当切线方程的斜率存在时,设方程为![]() ,则圆心到切线的距离
,则圆心到切线的距离![]() ,
,
化简得:![]() ,故
,故![]() .
.
∴切线方程为![]() ,
,
即![]() ,
,
当切线方程斜率不存在时,直线方程为![]() 与圆相切,
与圆相切,
综上,过点![]() 并与圆相切的切线方程为
并与圆相切的切线方程为![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=0,an+1=an+2 ![]() +1
+1
(1)求证数列{ ![]() }是等差数列,并求出an的通项公式;
}是等差数列,并求出an的通项公式;
(2)若bn= ![]() ,求数列{b}的前n项的和Tn .
,求数列{b}的前n项的和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第31届夏季奥林匹克运动会于2016年8月5日至8月21日在巴西里约热内卢举行.如表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
中国 | 38 | 51 | 32 | 28 | 16 |
俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(1)根据表格中两组数据在答题卡上完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(2)如表是近五届奥运会中国代表团获得的金牌数之和![]() (从第26届算起,不包括之前已获得的金牌数)随时间
(从第26届算起,不包括之前已获得的金牌数)随时间![]() 变化的数据:
变化的数据:
时间 | 26 | 27 | 28 | 29 | 30 |
金牌数之和 | 16 | 44 | 76 | 127 | 165 |
作出散点图如图:
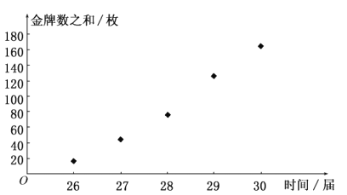
由图可以看出,金牌数之和![]() 与时间
与时间![]() 之间存在线性相关关系,请求出
之间存在线性相关关系,请求出![]() 关于
关于![]() 的线性回归方程,并预测从第26届到第32届奥运会时中国代表团获得的金牌数之和为多少?
的线性回归方程,并预测从第26届到第32届奥运会时中国代表团获得的金牌数之和为多少?
附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: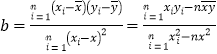 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() ,
,![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 上的点到曲线
上的点到曲线![]() 的距离的最大值和最小值.
的距离的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
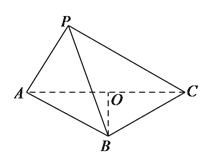
【题目】(![]() 分)如图,在三棱锥
分)如图,在三棱锥![]() 中,底面
中,底面![]() 为等边三角形,
为等边三角形,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(Ⅰ)求证:![]() .
.
(Ⅱ)判断在线段![]() 上是否存在点
上是否存在点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() 为直角三角形?若存在,试找出一个点
为直角三角形?若存在,试找出一个点![]() ,并求
,并求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中, ![]() ,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( )
,若利用下面程序框图计算该数列的第2016项,则判断框内的条件是( ) 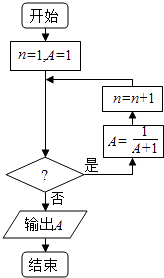
A.n≤2014
B.n≤2016
C.n≤2015
D.n≤2017
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
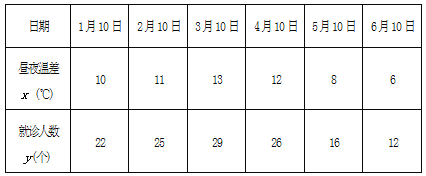
该兴趣小组确定的研究方案是:先用2、3、4、5月的4组数据求线性回归方程,再用1月和6月的2组数据进行检验.
(1)请根据2、3、4、5月的数据,求出y关于x的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:  ,
,![]()
 )
)
参考数据:11×25+13×29+12×26+8×16=![]() 1092,112+132+122+82=498.
1092,112+132+122+82=498.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 满足2Sn=an+1﹣2n+1+1,n∈N* , 且a1 , a2+5,a3成等差数列.
(1)求a1的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com