
����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ����Ԫ������������
����λ����Ԫ������������![]() ����λ���֣���Ӱ�죬�Խ��������������
����λ���֣���Ӱ�죬�Խ��������������![]() ����������
����������![]() (
(![]() )���������˳���ͳ�ƣ��õ��������ݣ�
)���������˳���ͳ�ƣ��õ��������ݣ�
��ݣ� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
�������� | 23 | 25 | 27 | 29 | 32 | 35 |
�������� | 11 | 21 | 24 | 66 | 115 | 325 |
��1������ɢ��ͼ�ж�![]() ��
��![]() ����һ�����ʺ���Ϊ��������
����һ�����ʺ���Ϊ��������![]() ���֣������������
���֣������������![]() ����Ԫ���Ļع鷽�����ͣ�
����Ԫ���Ļع鷽�����ͣ�
��2���涨����Ʒ����������![]() ���֣�����������
���֣�����������![]() ����Ԫ���ı�ֵ����1ʱ����Ϊ����Ч�����ã��ִ���6������ѡ3�꣬������ѡ��Ч�����õ�����Ϊ
����Ԫ���ı�ֵ����1ʱ����Ϊ����Ч�����ã��ִ���6������ѡ3�꣬������ѡ��Ч�����õ�����Ϊ![]() ������
������![]() ������ȡֵ�������Ӧ�ĸ��ʣ�
������ȡֵ�������Ӧ�ĸ��ʣ�
��3������Ƶ�ʷֲ�ֱ��ͼ�������������ƽ������˼�뷽������![]() ��ƽ����.
��ƽ����.
���𰸡���1��ɢ��ͼ����������2��![]() ��
��![]() ��
��![]() ��
��![]() ����3��
����3��![]() .
.
����������������1������ɢ��ͼ�������жϳ�.
��2���ɱ������ݿ�֪��Ч��������3�꣬��Ч��������ΪA��B��C���������Ϊ1��2��3��ö�ٷ��г�ȫ�����ܽ����20�֣��ٷֱ�ȷ����������Ч�����õ�����Ϊ![]() ������࣬���������Ӧ�ĸ��ʣ�
������࣬���������Ӧ�ĸ��ʣ�
��3������Ƶ�ʷֲ�ֱ��ͼ����������ƽ�����ķ����ã�![]() ���������
���������![]() ��ƽ����.
��ƽ����.
��⣺�⣺��1������ɢ��ͼ��֪������![]() �Ƚ����ˣ�
�Ƚ����ˣ�
��2���ü�6������3������Ч����������,
��6����Ч�����ݷֱ�Ϊ��A,B,C���������Ϊ1,2,3��6����ѡ3��IJ�ͬ����У�
ABC,AB1,AB2,AB3,AC1,AC2,AC3,BC1,BC2,BC3,A12,A13,A23,B12,B13,B23,C12,C13,C23��123��20�֣�
����![]() ��1�֣�����
��1�֣�����![]() ��
��
����![]() ��9�֣�����
��9�֣�����![]() ,
,
����![]() ��9�֣�����
��9�֣�����![]() ,
,
����![]() ��1�֣�����
��1�֣�����![]() ,
,
��3������Ƶ�ʷֲ�ֱ��ͼ����������ƽ�����ķ����ã�
![]() ��
��
��![]() ��ƽ����
��ƽ����![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѡ��4��4������ϵ��������̣�
��ֱ֪��l����P����1��2��������б��Ϊ ![]() ��Բ����Ϊ
��Բ����Ϊ ![]() ��
��
��1����ֱ��l�IJ������̣�
��2����ֱ��l��Բ����M��N���㣬��|PM||PN|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P-ABCD�У�����PAD�DZ߳�Ϊ2�ĵȱ��������Ҵ�ֱ�ڵ�![]() ��
�� ![]()
![]() ��
��![]() ���е㡣
���е㡣
��1��֤����ֱ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ����
����![]() �ϣ���ֱ��
�ϣ���ֱ��![]() �����
�����![]() ���ɽ�Ϊ
���ɽ�Ϊ![]() ��������
��������![]() ������ֵ��
������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й�ƹ����ӱ�ս��Լ���˻���������ѡ������2016��7��14����ɽ����������������ѡ��A�������ѡ��B1 �� B2 �� B3�ֱ����һ���Կ�������������α�����ͳ�ƣ�A��ʤ�ĸ��ʷֱ�Ϊ ![]() ���Ҹ�����������Ӱ�죮
���Ҹ�����������Ӱ�죮
������A���ٻ�ʤ�����ĸ��ʴ��� ![]() ����A��ѡ��ս��Լ���˻��������������������ѡ����A�Ƿ����ѡ���յ�������
����A��ѡ��ս��Լ���˻��������������������ѡ����A�Ƿ����ѡ���յ�������
������A��ʤ����X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
��1������![]() ����С�����ڣ�
����С�����ڣ�
��2������![]() �ĵ����������估�Գ����ģ�
�ĵ����������估�Գ����ģ�
��3������![]() ������
������![]() ���������ı任�õ�.
���������ı任�õ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ͬѧ���ô��ڽ������ʵ�����Ա���![]() �����Ⱥ�����ȡ
�����Ⱥ�����ȡ![]() �˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�塱�������Ϊ���ǵ�̼�塱���õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��
�˽�����һ������ϰ���Ƿ���ϵ�̼����ĵ��飬������ϰ�߷��ϵ�̼����ij�Ϊ����̼�塱�������Ϊ���ǵ�̼�塱���õ�����ͳ�Ʊ������������Ƶ�ʷֲ�ֱ��ͼ��

��һ������ͳ�Ʊ��� �����������������Ƶ�ʷֲ�ֱ��ͼ��
�����ڴ������������ϵ�в�ȫƵ�ʷֲ�ֱ��ͼ�������![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
����![]() ������εġ���̼�塱�в��÷ֲ��������ȡ
������εġ���̼�塱�в��÷ֲ��������ȡ![]() �˲μӻ����̼������������
�˲μӻ����̼������������![]() ����ͨ����ǩ�ֳɼס������飬ÿ���������ͬ����
����ͨ����ǩ�ֳɼס������飬ÿ���������ͬ����![]() ���б���ȡ����ǡ���ַ���ͬһ��ĸ��ʡ�
���б���ȡ����ǡ���ַ���ͬһ��ĸ��ʡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Ʒ![]() �����������ۺ�ָ��ֵ
�����������ۺ�ָ��ֵ![]() ���к�����
���к�����![]() Ϊһ��Ʒ��
Ϊһ��Ʒ��![]() Ϊ����Ʒ��
Ϊ����Ʒ��![]() Ϊ����Ʒ.����һ�ҹ��������������豸�����������Ʒ
Ϊ����Ʒ.����һ�ҹ��������������豸�����������Ʒ![]() ��Ч�棬��ij��Ӧ���ṩ���豸����ѡһ�����ã�������һ����Ʒ��ͳ��������ݣ��õ�Ƶ�ʷֲ�ֱ��ͼ��
��Ч�棬��ij��Ӧ���ṩ���豸����ѡһ�����ã�������һ����Ʒ��ͳ��������ݣ��õ�Ƶ�ʷֲ�ֱ��ͼ��
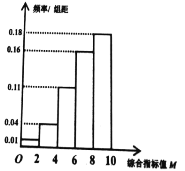
��1�����Ƹ������豸�����IJ�Ʒ![]() Ϊ����Ʒ�ĸ��ʣ�
Ϊ����Ʒ�ĸ��ʣ�
��2��������ҹ����ļ�¼����Ʒ���ȴε������ʣ�ij�ȴβ�Ʒ���������Ӧ�����ı�ֵ���������ۼ�������£�
һ��Ʒ | ����Ʒ | ����Ʒ | |
������ |
|
|
|
�����ۼ� |
|
|
|
�������������۷�����δ�۳��IJ�Ʒͳһ��ԭ�ۼ۵�![]() ȫ��������.��֪�ù����Ϲ��������豸��ǰ�������ǣ��������豸�����IJ�Ʒͬʱ������������������
ȫ��������.��֪�ù����Ϲ��������豸��ǰ�������ǣ��������豸�����IJ�Ʒͬʱ������������������
���ۺ�ָ��ֵ��ƽ������С��![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
�ڵ���ƽ������ֵ������![]() .
.
���������豸�����IJ�Ʒ![]() �ijɱ�Ϊ
�ijɱ�Ϊ![]() Ԫ/�����²���Ϊ
Ԫ/�����²���Ϊ![]() ���������۷������������£���������ͼ�����ݣ������������豸�Ƿ�ﵽ�ù������Ϲ�����.
���������۷������������£���������ͼ�����ݣ������������豸�Ƿ�ﵽ�ù������Ϲ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��
��
��1����f��x���ļ�ֵ��
��2����0��x��eʱ����֤��f��e+x����f��e��x����
��3���躯��f��x��ͼ����ֱ��y=m��������ֱ�ΪA��x1 �� f��x1����B��x2 �� f��x2�������е������Ϊx0 �� ֤����f'��x0����0��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com