
【题目】已知函数f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )(x∈R),则下面结论错误的是( )
)(x∈R),则下面结论错误的是( )
A.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
B.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
C.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
D.函数f(x)的图象是由函数y= ![]() sin2x的图象向右平移
sin2x的图象向右平移 ![]() 个单位而得到
个单位而得到
【答案】A
【解析】解:∵函数f(x)=sin(x﹣ ![]() )cos(x﹣
)cos(x﹣ ![]() )=
)= ![]() sin(2x﹣
sin(2x﹣ ![]() ),令x=﹣
),令x=﹣ ![]() ,可得2x﹣
,可得2x﹣ ![]() =﹣
=﹣ ![]() ,f(x)≠0,
,f(x)≠0,
故函数f(x)的图象不关于点(﹣ ![]() ,0)对称,故A错误.
,0)对称,故A错误.
令x=﹣ ![]() ,可得2x﹣
,可得2x﹣ ![]() =﹣
=﹣ ![]() ,f(x)=0,故函数f(x)的图象关于点(﹣
,f(x)=0,故函数f(x)的图象关于点(﹣ ![]() ,0)对称,故B正确.
,0)对称,故B正确.
令x∈[0, ![]() ],可得2x﹣
],可得2x﹣ ![]() ∈[﹣
∈[﹣ ![]() ,
, ![]() ],故函数f(x)在区间[0,
],故函数f(x)在区间[0, ![]() ]上是增函数,故C正确.
]上是增函数,故C正确.
把函数y= ![]() sin2x的图象向右平移
sin2x的图象向右平移 ![]() 个单位,可得y=
个单位,可得y= ![]() sin(2x﹣
sin(2x﹣ ![]() ) 的图象,故D正确,
) 的图象,故D正确,
故选:A.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么由此求出的平均数与实际平均数的差是( )
A.35
B.﹣3
C.3
D.﹣0.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+ ![]() )升,司机的工资是每小时14元.
)升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【广西名校2017届高三上学期第一次摸底】如图,过抛物线![]() 上一点
上一点![]() ,作两条直线分别交抛物线于
,作两条直线分别交抛物线于![]() ,
,![]() ,
,
当![]() 与
与![]() 的斜率存在且倾斜角互补时:
的斜率存在且倾斜角互补时:
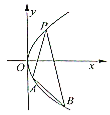
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 时,求
时,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x、y)满足
(1)若x∈{0,1,2,3,4,5},y∈{0,1,2,3,4},则求y≥x的概率.
(2)若x∈[0,5],y∈[0,4],则求x>y的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为椭圆
为椭圆![]() 的左右焦点,点
的左右焦点,点![]() 为其上一点,且有
为其上一点,且有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,过
两点,过![]() 与
与![]() 平行的直线
平行的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 的面积
的面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
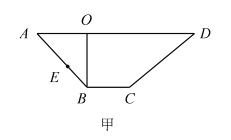
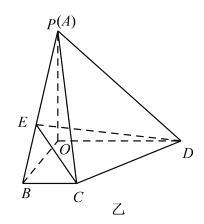
【题目】如图甲所示, ![]() 是梯形
是梯形![]() 的高,
的高, ![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起如图乙所示的四棱锥
折起如图乙所示的四棱锥![]() ,使得
,使得![]() ,点
,点![]() 是线段
是线段![]() 上一动点.
上一动点.
(1)证明: ![]() 和
和![]() 不可能垂直;
不可能垂直;
(2)当![]() 时,求
时,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com