
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点,试判断函数
有两个极值点,试判断函数![]() 的零点个数.
的零点个数.
【答案】(1) 当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减;(2)存在3个零点.
单调递减;(2)存在3个零点.
【解析】
(1)先确定![]() 的定义域,通过求导数解出其单调区间;
的定义域,通过求导数解出其单调区间;
(2)利用函数![]() 有极值,判断
有极值,判断![]() 的取值范围,进而确定极值点的大小关系,得到
的取值范围,进而确定极值点的大小关系,得到![]() 的单调区间,最后通过极值
的单调区间,最后通过极值![]() 的正负判断出零点的个数.
的正负判断出零点的个数.
(1)由题意可知函数![]() 的定义域为
的定义域为![]()
当![]() 时:
时:![]() ,所以
,所以![]() 单调递增;
单调递增;
当![]() 时:
时:![]() ,所以
,所以![]() 单调递减;
单调递减;
所以当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减.
单调递减.
(2)由题意得:![]() 有两个不同的零点,即
有两个不同的零点,即![]() 有两个不同的根设为
有两个不同的根设为![]() ,由(1)得
,由(1)得![]() 当
当![]() 时
时![]() 单调递增;当
单调递增;当![]() 时
时![]() 单调递减;有
单调递减;有![]() 当
当![]() 时
时![]() ,所以
,所以![]() 时,有
时,有![]() 使
使![]() 且函数
且函数![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增,
单调递增,
现只需比较![]() 的正负进而确定零点个数.
的正负进而确定零点个数.
有![]() 且
且![]() 且
且![]() ,即
,即![]() ,
,![]() .
.
令![]() 则
则 所以函数
所以函数![]() 在
在![]() 上单调增,所以
上单调增,所以![]() 时
时![]()
![]() 时
时![]() 又
又![]() 时
时![]() 时
时![]()
所以函数有三个零点.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,若满足
,若满足![]() ,则称函数
,则称函数![]() 为“
为“![]() 型函数”.
型函数”.
(1)判断函数![]() 和
和![]() 是否为“
是否为“![]() 型函数”,并说明理由;
型函数”,并说明理由;
(2)设函数![]() ,记
,记![]() 为函数
为函数![]() 的导函数.
的导函数.
①若函数![]() 的最小值为1,求
的最小值为1,求![]() 的值;
的值;
②若函数![]() 为“
为“![]() 型函数”,求
型函数”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学组织高二年级开展对某品牌西瓜市场调研活动.两名同学经过了解得知此品牌西瓜,不仅便宜而且口味还不错,并且每日的销售量y(单位:千克)与销售价格x(元/千克)满足关系式:![]() ,其中
,其中![]() ,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
,a为常数.已知销售价格为5元/千克时,每日可售出此品牌西瓜11千克.若此品牌西瓜的成本为3元/千克,试确定销售价格x的值,使该商场日销售此品牌西瓜所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四面体![]() 的棱长满足
的棱长满足![]() ,
,![]() ,现将四面体
,现将四面体![]() 放入一个主视图为等边三角形的圆锥中,使得四面体
放入一个主视图为等边三角形的圆锥中,使得四面体![]() 可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
可以在圆锥中任意转动,则圆锥侧面积的最小值为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
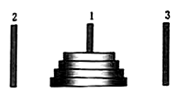
【题目】如图所示,有三根针和套在一根针上的![]() 个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
个金属片,按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面.
将![]() 个金属片从1号针移到3号针最少需要移动的次数记为
个金属片从1号针移到3号针最少需要移动的次数记为![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与x轴负半轴交于
与x轴负半轴交于![]() ,离心率
,离心率![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() 与椭圆C交于
与椭圆C交于![]() 两点,连接AM,AN并延长交直线x=4于
两点,连接AM,AN并延长交直线x=4于![]() 两点,若
两点,若![]() ,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
,直线MN是否恒过定点,如果是,请求出定点坐标,如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100名学生的数学成绩,发现都在![]() 内现将这100名学生的成绩按照
内现将这100名学生的成绩按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组后,得到的频率分布直方图如图所示,则下列说法正确的是
分组后,得到的频率分布直方图如图所示,则下列说法正确的是![]()
![]()

A. 频率分布直方图中a的值为![]()
B. 样本数据低于130分的频率为![]()
C. 总体的中位数![]() 保留1位小数
保留1位小数![]() 估计为
估计为![]() 分
分
D. 总体分布在![]() 的频数一定与总体分布在
的频数一定与总体分布在![]() 的频数相等
的频数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() ,以原点为极点,
,以原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为曲线
的极坐标方程为曲线![]() .
.
(Ⅰ)写出直线![]() 的参数方程及曲线
的参数方程及曲线![]() 的普通方程;
的普通方程;
(Ⅱ)求直线![]() 和曲线
和曲线![]() 的两个交点到点
的两个交点到点![]() 的距离的和与积.
的距离的和与积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com