
【题目】在四棱锥![]() 中,
中,![]() ,
,![]() .
.

(Ⅰ)若点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)当平面![]() 平面
平面![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(I)结合平面与平面平行判定,得到平面BEM平行平面PAD,结合平面与平面性质,证明结论.(II)建立空间坐标系,分别计算平面PCD和平面PDB的法向量,结合向量数量积公式,计算余弦值,即可.
(Ⅰ)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]() .
.
由已知得,![]() 为等边三角形,
为等边三角形,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .
.
∵![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,∴
的中点,∴![]() ∥
∥![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ∥平面
∥平面![]() .
.
∵![]() ,∴平面
,∴平面![]() ∥平面
∥平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]() .
.
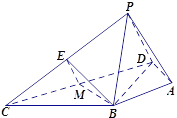
(Ⅱ)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,由对称性知,
,由对称性知,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴正方向,建立空间直角坐标系
轴正方向,建立空间直角坐标系![]() .
.
则![]() (0,
(0,![]() ,0),
,0),![]() (3,0,0),
(3,0,0),![]() (0,0,1).
(0,0,1).
易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,
,![]() ,∴
,∴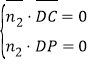 ,
,
∵![]() ,
,![]() ,∴
,∴![]() .
.
令![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴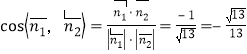 .
.
设二面角![]() 的大小为
的大小为![]() ,则
,则![]() .
.


科目:高中数学 来源: 题型:
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校或班级举行活动,通常需要张贴海报进行宣传.现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128 dm2,上、下两边各空2 dm,左、右两边各空1 dm.如何设计海报的尺寸,才能使四周空白面积最小?
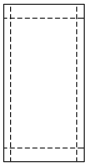
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)若函数![]() 在区间
在区间![]() 上是单调函数,试求实数
上是单调函数,试求实数![]() 的取值范围;
的取值范围;
(2)已知函数![]() ,且
,且![]() ,若函数
,若函数![]() 在区间
在区间![]() 上恰有3个零点,求实数
上恰有3个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() 与该小卖部的这种饮料销量
与该小卖部的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(1)中所得的线性回归方程,若天气预报1月16日的白天平均气温![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.

(Ⅰ)求直方图中a的值;
(Ⅱ)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(Ⅲ)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() R.
R.
(1)证明:当![]() 时,函数
时,函数![]() 是减函数;
是减函数;
(2)根据![]() 的不同取值,讨论函数
的不同取值,讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)当![]() ,且
,且![]() 时,证明:对任意
时,证明:对任意![]() ,存在唯一的
,存在唯一的![]() R,使得
R,使得![]() ,且
,且![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com