Question

【题目】如图所示，该几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成，AD⊥AF，AE=AD=2．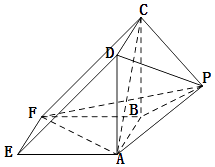
（Ⅰ）证明：平面PAD⊥平面ABFE；
（Ⅱ）求正四棱锥P﹣ABCD的高h，使得二面角C﹣AF﹣P的余弦值是 ．

Answer 1

【答案】证明：（Ⅰ）∵几何体是由一个直三棱柱ADE﹣BCF和一个正四棱锥P﹣ABCD组合而成，

∴AD⊥AF，AD⊥AB，

又AF∩AB=A，

∴AD⊥平面ABEF，

又AD平面PAD，

∴平面PAD⊥平面ABFE．

解：（Ⅱ）以A 为原点，AB、AE、AD的正方向为x，y，z轴，建立空间直角坐标系A﹣xyz

设正四棱棱的高为h，AE=AD=2，

则A（0，0，0），F（2，2，0），C（2，0，2），P（1，﹣1，1）

设平面ACF的一个法向量 =（x，y，z），

=（2，2，0）， =（2，0，2），

则 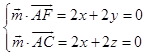，取x=1，得 =（1，﹣1，﹣1），

设平面ACP的一个法向量 =（a，b，c），

则 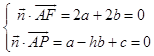，取b=1，则 =（﹣1，1，1+h），

二面角C﹣AF﹣P的余弦值 ，

∴|cos＜ ＞|= = = ，

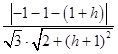解得h=1．

【解析】
【考点精析】关于本题考查的平面与平面垂直的判定，需要了解一个平面过另一个平面的垂线，则这两个平面垂直才能得出正确答案．