
【题目】如图,正三棱柱![]() 的底面边长为3,侧棱
的底面边长为3,侧棱![]() ,D是CB延长线上一点,且
,D是CB延长线上一点,且![]() .
.
![]() 求二面角
求二面角![]() 的正切值;
的正切值;
![]() 求三棱锥
求三棱锥![]() 的体积.
的体积.

【答案】(1)2(2)![]()
【解析】
![]() 取BC中点O,
取BC中点O,![]() 中点E,连结OE,OA,以O为原点,OD为x轴,OE为y轴,OA为z轴,建立空间直角坐标系,利用向量法能求出二面角
中点E,连结OE,OA,以O为原点,OD为x轴,OE为y轴,OA为z轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的正切值.
的正切值.
![]() 三棱锥
三棱锥![]() 的体积
的体积![]() ,由此能求出结果.
,由此能求出结果.
![]() 取BC中点O,
取BC中点O,![]() 中点E,连结OE,OA,
中点E,连结OE,OA,
由正三棱柱![]() 的底面边长为3,侧棱
的底面边长为3,侧棱![]() ,D是CB延长线上一点,且
,D是CB延长线上一点,且![]() .
.
以O为原点,OD为x轴,OE为y轴,OA为z轴,建立空间直角坐标系,
则![]() 3,
3,![]() ,
,![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,![]() 0,
0,![]() ,
,
所以![]() 0,
0,![]() ,
,![]() 3,
3,![]() ,
,
其中平面ABD的法向量![]() 1,
1,![]() ,
,
设平面![]() 的法向量
的法向量![]() y,
y,![]() ,则
,则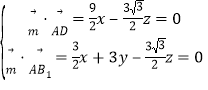 ,
,
取![]() ,得
,得![]() 1,
1,![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,则
,则![]() ,则
,则![]() ,
,
则![]() ,所以二面角
,所以二面角![]() 的正切值为2.
的正切值为2.
![]() 由(1)可得
由(1)可得![]() 平面
平面![]() ,所以
,所以![]() 是三棱锥
是三棱锥![]() 的高,且
的高,且![]() ,
,
所以三棱锥![]() 的体积:
的体积:
![]() .
.


科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,则下列命题正确的是 . (填写所有正确命题的序号) ①若sinAsinB=2sin2C,则0<C< ![]() ;
;
②若a+b>2c,则0<C< ![]() ;
;
③若a4+b4=c4 . 则△ABC为锐角三角形;
④若(a+b)c<2ab,则C> ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了检查一条流水线的生产情况,从该流水线上随机抽取40件产品,测量这些产品的重量(单位:克),整理后得到如下的频率分布直方图(其中重量的分组区间分别为(490,495],(495,500],(500,505],(505,510],(510,515]) (I)若从这40件产品中任取两件,设X为重量超过505克的产品数量,求随机变量X的分布列;
(Ⅱ)若将该样本分布近似看作总体分布,现从该流水线上任取5件产品,求恰有两件产品的重量超过505克的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com